题目内容
【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
(1)观察猜想
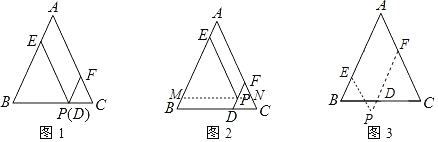
如图1,当点P在BC边上时,此时点P、D重合,试猜想PD,PE,PF与AB的数量关系: .
(2)类比探究
如图2,当点P在△ABC内时,过点P作MN∥BC交AB于点M,交AC于点N,试写出PD,PE,PF与AB的数量关系,并加以证明.
(3)解决问题
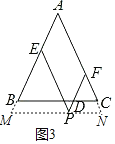
如图3,当点P在△ABC外时,若AB=6,PD=1,请直接写出平行四边形PEAF的周长 .
【答案】(1)PD+PE+PF=AB;(2)PD+PE+PF=AB,见解析;(3)14
【解析】
(1)由PE∥AC,PF∥AB可判断四边形AEPF为平行四边形,根据平行线的性质得∠1=∠C,根据平行四边形的性质得PF=AE,再根据等腰三角形的性质得∠B=∠C,则∠B=∠1,则可根据等腰三角形的判定得PE=BE,所以PE+PF=AB;
(2)因为四边形PEAF为平行四边形,所以PE=AF,又三角形FDC为等腰三角形,所以FD=PF+PD=FC,即PE+PD+PF=AC=AB;
(3)过点P作MN∥BC分别交AB、AC于M、N两点,推出PE+PF=AM,再推出MB=PD即可得到结论.
解:(1)答:PD+PE+PF=AB.
证明如下:∵点P在BC上,
∴PD=0,
∵PE∥AC,PF∥AB,
∴四边形PFAE是平行四边形,
∴PF=AE,
∵PE∥AC,
∴∠BPE=∠C,
∴∠B=∠BPE,
∴PE=BE,
∴PE+PF=BE+AE=AB,
∵PD=0,
∴PD+PE+PF=AB,
故答案为:PD+PE+PF=AB;
(2)如图2,结论成立:PD+PE+PF=AB.

证明:过点P作MN∥BC分别交AB,AC于M,N两点,
∵PE∥AC,PF∥AB,
∴四边形AEPF是平行四边形,
∵MN∥BC,PF∥AB,
∴四边形BDPM是平行四边形,
∴AE=PF,∠EPM=∠ANM=∠C,
∵AB=AC,
∴∠EMP=∠B,
∴∠EMP=∠EPM,
∴PE=EM,
∴PE+PF=AE+EM=AM.
∵四边形BDPM是平行四边形,
∴MB=PD.
∴PD+PE+PF=MB+AM=AB,
即PD+PE+PF=AB;
(3)如图3,过点P作MN∥BC分别交AB、AC延长线于M、N两点.
∵PE∥AC,PF∥AB,
∴四边形PEAF是平行四边形,
∴PF=AE,
∵AB=AC,
∴∠B=∠C,
∵MN∥BC,
∴∠ANM=∠C=∠B=∠AMN,
∵PE∥AC,
∴∠EPM=∠FNP,
∴∠AMN=∠FPN,
∴∠EPM=∠EMP,
∴PE=ME,
∵AE+ME=AM,
∴PE+PF=AM,
∵MN∥CB,DF∥AB,
∴四边形BDPM是平行四边形,
∴MB=PD,
∴PE+PF﹣PD=AM﹣MB=AB,
∴PE+PF=AB+PD=6+1=7,
∴平行四边形PEAF的周长=14,
故答案为:14.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案