题目内容
【题目】如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线。
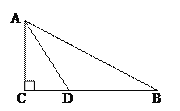
(1)以AB上一点O为圆心,AD为弦作⊙O;
(2)求证:BC为⊙O的切线;
(3)如果AC=3,tanB=![]() ,求⊙O的半径。
,求⊙O的半径。
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:
(1)由题意可知,作线段AD的垂直平分线与AB相交,交点即为圆心O,然后以O为圆心OA为半径作圆即可;
(2)连接OD,由已知易证∠ODA=∠OAD=∠CAD,从而可得OD∥AC,由此可得∠ODB=∠C=90°,结合OD是⊙O的半径即可得到BC和⊙O相切;
(3)由已知条件易得BC=4和AB=5的长度,设⊙O的半径为r,则OD=OA=r,OB=5-r;由OD∥AC可得△BDO∽△BCA,这样由相似三角形对应边成比例即可列出关于r的方程,解方程即可求得r的值.
试题解析:
(1)如图所示,⊙O为所求圆;
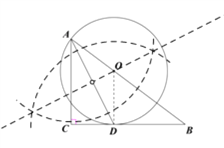
(2)连接OD.
∵AD平分∠CAB
∴∠CAD=∠BAD
又∵OA=OD
∴∠OAD=∠ODA
∴∠CAD=∠ODA
∴OD∥AC
∴∠ODB=∠C=90°
又∵OD为半径
∴BC是⊙O的切线.
(3)∵在△ABC中,AC=3,tanB=![]() ,∠C=90°,
,∠C=90°,
∴BC=4,AB=5,
设⊙O的半径为r,则OA=OD=r,BO=5-r
∵OD∥AC
∴△BOD∽△BAC
∴![]()
即 ![]()
解得, ![]() ,
,
∴⊙O的半径为 ![]() .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目