题目内容
【题目】已知：直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD，H，P分别为直线AB和线段EF上的点。
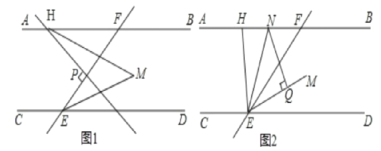
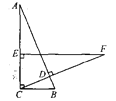
(1)如图1，HM平分∠BHP，若HP⊥EF，求∠M的度数。
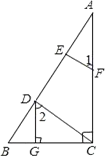
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时，探究∠FHE与∠ENQ的关系，并证明你的结论。
【答案】（1）45o （2）∠FHE=2∠ENQ或∠FHE=180°2∠ENQ，证明见解析
【解析】
（1）首先作MQ∥AB，根据平行线的性质，推得∠M=
（∠FHP+∠HFP）；然后根据HP⊥EF，推得∠FHP+∠HFP=90°，据此求出∠M的度数即可．
（2）①如图2，首先判断出∠NEQ=∠NEF+∠QEF=（∠HEF+∠DEF）=∠HED，然后根据NQ⊥EM，可得∠NEQ+∠ENQ=90°，推得∠ENQ=（180°-∠HED）=∠CEH，再根据AB∥CD，推得∠FHE=2∠ENQ即可．
②如图3，首先判断出∠NEQ=∠QEF-∠NEF=（∠DEF-∠HEF）=∠HED，然后根据NQ⊥EM，可得∠NEQ+∠ENQ=90°，推得∠ENQ=（180°-∠HED）=∠CEH，再根据AB∥CD，推得∠FHE=180°-2∠ENQ即可．
如图1,作MQ∥AB,
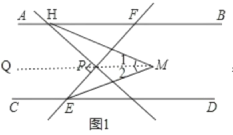
∵AB∥CD,MQ∥AB，
∴MQ∥CD，
∴∠1=∠FHM，∠2=∠DEM，
∴∠1+∠2=∠FHM+∠DEM= (∠FHP+∠FED)= (∠FHP+∠HFP)，
∵HP⊥EF，
∴∠HPF=90°，
∴∠FHP+∠HFP=180°90°=90°，
∵∠1+∠2=∠M，
∴∠M=×90°=45°.
(2)①如图2,
∠FHE=2∠ENQ，理由如下：
∠NEQ=∠NEF+∠QEF= (∠HEF+∠DEF)= ∠HED，
∵NQ⊥EM，
∴∠NEQ+∠ENQ=90°，
∴∠ENQ=
(180°∠HED)= ∠CEH，
∵AB∥CD，
∴∠FHE=∠CEH=2∠ENQ.
②如图3,
∠FHE=180°2∠ENQ，理由如下：
∠NEQ=∠QEF∠NEF= (∠DEF∠HEF)= ∠HED，
∵NQ⊥EM，
∴∠NEQ+∠ENQ=90°，
∴∠ENQ= (180°∠HED)= ∠CEH，
∵AB∥CD，
∴∠FHE=180°∠CEH=180°2∠ENQ.
综上，可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°2∠ENQ.
