题目内容
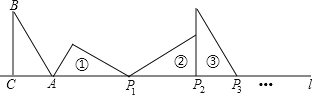
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,且AC在直线1上,将△ABC绕点A顺时针旋转到位置①,可得到点P1,将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,…,按此规律继续旋转,得到点P2018为止,则AP2018=___.
【答案】8073
【解析】
观察不难发现,每旋转3次为一个循环组依次循环,用2018除以3求出循环组数,然后列式计算即可得解.
∵Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,
∴将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=5;
将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=5+4=9;
将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=5+4+3=12;
又∵2018÷3=672…2,
∴AP2018=672×12+(5+4)=8064+9=8073.
故答案为:8073.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目