题目内容
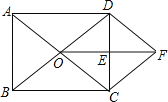
【题目】如图所示，在△ABD中，∠A是直角，AB=3，AD=4，BC=12，DC=13，求四边形ABCD的面积.
【答案】36
【解析】试题分析：根据勾股定理求得BD=5；由勾股定理的逆定理判定△BCD为直角三角形，则四边形ABCD的面积=△ABD的面积+△BCD的面积．
试题解析：∵在△ABD中，∠A是直角，AB=3，AD=4，
∴由勾股定理得 BD2=AD2+AB2=25．则BD=5，
又∵在△BCD中，BC=12，DC=13，
∴CD2=BD2+BC2=169，
∴△BCD为直角三角形，且∠DBC=90°，
∴S四边形ABCD=S△ABD+S△BCD=
ADAB+
BDBC=
×4×3+
×5×12=36．
即四边形ABCD的面积是36．
考点: 1.勾股定理；2.勾股定理的逆定理．
练习册系列答案
相关题目
【题目】小明在某一次实验中，测得两个变量之间的关系如下表所示：
x | 1 | 2 | 3 | 4 | 12 | |
y | 12.03 | 5.98 | 3.03 | 1.99 | 1.00 |
请你根据表格回答下列问题：
①这两个变量之间可能是怎样的函数关系？你是怎样作出判断的？请你简要说明理由；
②请你写出这个函数的解析式；
③表格中空缺的数值可能是多少？请你给出合理的数值．
