题目内容
【题目】如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=﹣ ![]() x2﹣2x+c经过点A、B,抛物线的顶点为C.
x2﹣2x+c经过点A、B,抛物线的顶点为C.
(1)∠BAO=°;
(2)求tan∠CAB的值;
(3)在抛物线上是否存在点P,能够使∠PCA=∠BAC?如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】
(1)45
(2)
解:由(1)得:B(0,n),A(﹣n,0),
∵抛物线y=﹣ ![]() x2﹣2x+c经过点A、B
x2﹣2x+c经过点A、B
∴  ,解得
,解得 ![]() 或
或 ![]() (舍去)
(舍去)
∴A(﹣6,0),B(0,6),直线AB的解析式为:y=x+6,
抛物线为:y=﹣ ![]() ﹣2x+6=﹣
﹣2x+6=﹣ ![]() (x+2)2+8,
(x+2)2+8,
∴抛物线的顶点为C(﹣2,8),
设抛物线的对称轴为直线l,连结BC,
如图1,过点B作BD⊥l,则BD=CD=2,BD∥x轴,
∴∠CBD=45°,
又BD∥x轴,
∴∠DBA=∠BAO=45°,
∴∠CBA=∠CBD+∠DBA=90°,
在Rt△CDB中,BC= ![]() =2
=2 ![]() ,
,
在Rt△AOB中,AB= ![]() =6
=6 ![]() ,
,
∴在Rt△ABC中,tan∠CAB= ![]() =
= ![]()

(3)
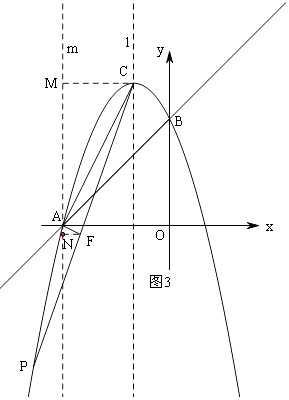
解:①当点P在CA左侧时,如图2,
延长BD交抛物线于点E,当∠PCA=∠BAC时,CP∥AB,
此时,点P与点E重合,点P的坐标是(﹣4,6);
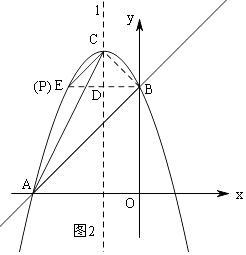
②当点P在CA右侧时,如图3,过点A作AC的垂线交CP于点F,
过点A作y轴的平行线m,过点C作CM⊥m,过点F作FN⊥m,
由于tan∠BAC= ![]() ,所以tan∠ACF=tan∠ACP=
,所以tan∠ACF=tan∠ACP= ![]() ,
,
∵Rt△CMA∽Rt△ANF,
∴ ![]() ,
, ![]() ,AN=
,AN= ![]() CM=
CM= ![]() ,NF=
,NF= ![]() MA=
MA= ![]() ,
,
∴F(﹣ ![]() ,﹣
,﹣ ![]() );
);
易求得直线CF的解析式为:y=7x+22,
由 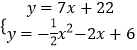 ,消去y,得x2+18x+32=0,
,消去y,得x2+18x+32=0,
解得x=16或x=﹣2(舍去),
因此点P的坐标(﹣16,﹣90);
综上所述,P的坐标是(﹣4,6)或(﹣16,﹣90).
【解析】解:(1)y=x+n,
当x=0时,y=n,则B(0,n),
当y=0时,x=﹣n,则A(﹣n,0),
∴OA=OB=n,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
所以答案是:45;