题目内容
【题目】如图,直线y= ![]() x﹣
x﹣ ![]() 与x,y轴分别交于点A,B,与反比例函数y=
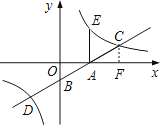
与x,y轴分别交于点A,B,与反比例函数y= ![]() (k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
(1)求点A的坐标.
(2)若AE=AC.
①求k的值.
②试判断点E与点D是否关于原点O成中心对称?并说明理由.
【答案】
(1)
解:当y=0时,得0= ![]() x﹣
x﹣ ![]() ,解得:x=3.
,解得:x=3.
∴点A的坐标为(3,0)
(2)
解:①过点C作CF⊥x轴于点F,如图所示.
设AE=AC=t,点E的坐标是(3,t),
在Rt△AOB中,tan∠OAB= ![]() =
= ![]() ,
,
∴∠OAB=30°.
在Rt△ACF中,∠CAF=30°,
∴CF= ![]() t,AF=ACcos30°=
t,AF=ACcos30°= ![]() t,
t,
∴点C的坐标是(3+ ![]() t,
t, ![]() t).
t).
∴(3+ ![]() t)×
t)× ![]() t=3t,
t=3t,
解得:t1=0(舍去),t2=2 ![]() .
.
∴k=3t=6 ![]() .
.
②点E与点D关于原点O成中心对称,理由如下:
设点D的坐标是(x, ![]() x﹣
x﹣ ![]() ),
),
∴x( ![]() x﹣
x﹣ ![]() )=6
)=6 ![]() ,解得:x1=6,x2=﹣3,
,解得:x1=6,x2=﹣3,
∴点D的坐标是(﹣3,﹣2 ![]() ).
).
又∵点E的坐标为(3,2 ![]() ),
),
∴点E与点D关于原点O成中心对称
【解析】(1)令一次函数中y=0,解关于x的一元一次方程,即可得出结论;(2)①过点C作CF⊥x轴于点F,设AE=AC=t,由此表示出点E的坐标,利用特殊角的三角形函数值,通过计算可得出点C的坐标,再根据反比例函数图象上点的坐标特征可得出关于t的一元二次方程,解方程即可得出结论;
②根据点在直线上设出点D的坐标,根据反比例函数图象上点的坐标特征可得出关于点D横坐标的一元二次方程,解方程即可得出点D的坐标,结合①中点E的坐标即可得出结论.本题考查了反比例函数与一次函数的交点问题、解一元二次方程以及反比例函数图象上点的坐标特征,解题的关键是:(1)令一次函数中y=0求出x的值;(2)根据反比例函数图象上点的坐标特征得出一元二次方程.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数图象上点的坐标特征找出关于点的横坐标的一元二次方程是关键.

【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
学生人数(人) | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm



