题目内容
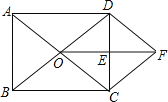
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据两直线平行,内错角相等可得∠ODE=∠FCE,根据线段中点的定义可得CE=DE,然后利用“角边角”证明△ODE和△FCE全等;
(2)根据全等三角形对应边相等可得OD=FC,再根据一组对边平行且相等的四边形是平行四边形判断出四边形ODFC是平行四边形,根据矩形的对角线互相平分且相等可得OC=OD,然后根据邻边相等的平行四边形是菱形证明即可.
试题解析:(1)∵CF∥BD
∴∠DOE=∠CFE,
∵E是CD的中点,
∴CE=DE
在△ODE和△FCE中,
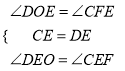 ,
,
∴△ODE≌△FCE(ASA)
∴OD=CF.
(2)由(1)知OD=CF ,
∵CF∥BD ,
∴四边形ODFC是平行四边形
在矩形ABCD中,OC=OD,
∴四边形ODFC是菱形.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
等级 | 人数/名 |
优秀 | a |
良好 | b |
及格 | 150 |
不及格 | 50 |
解答下列问题:
(1)a等于多少?,b等于多少?
(2)补全条形统计图;
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.

【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.