Question

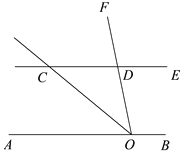
【题目】如图，在直角坐标系内，一次函数y＝kx＋b(k＜0，b<0)的图象分别与x轴、y轴和直线x＝4相交于A，B，C三点，直线x＝4与x轴交于点D，四边形OBCD(O是坐标原点)的面积是10，若点A的横坐标是－，求这个一次函数表达式．

Answer 1

【答案】一次函数的表达式为y＝－x－

【解析】试题分析：由题意确定出A的坐标，代入一次函数解析式得到关于k与b的方程，表示出B与C的坐标，利用梯形面积公式表示出四边形OBCD面积，将已知面积代入得到关于k与b的方程，联立求出k与b的值，即可确定出一次函数解析式．

试题解析：解：由A的横坐标为﹣，得到A（﹣，0），把A坐标代入一次函数y=kx+b解析式得：﹣k+b=0①，令x=0，得到：y=b，即B（0，b），令x=4，得到：y=4k+b，即C（4，4k+b）．∵S四边形OBCD=（OB+CD）OD=10，即×（﹣b﹣4k﹣b）×4=10，∴4k+2b=﹣5②，联立①②，解得：k=﹣1，b=﹣，则一次函数解析式为y=﹣x﹣．