题目内容
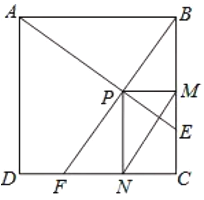
【题目】如图,已知矩形![]() ,点
,点![]() 是对角线
是对角线![]() 上一点,连结
上一点,连结![]() ,作
,作![]() ,交
,交![]() 于
于![]() ,
,
(1)若![]() ,
,![]() 则
则![]() ________________.
________________.
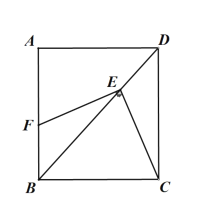
(2)连结![]() 若
若![]() ,则
,则![]() ________________.
________________.
【答案】![]() 1
1
【解析】
(1)过E点作AB的垂线,由正方形性质可得![]() ,解
,解![]() 可得
可得![]() ,再证明
,再证明![]() ,从而可得FG=EH,进而求出
,从而可得FG=EH,进而求出![]() ,即可求出比值.
,即可求出比值.
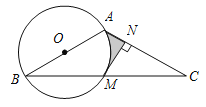
(2)由![]() ,可得
,可得![]() ,而
,而![]() ,故FC垂直BD,有BEFC四点共圆而且FC为直径,由垂径定理可推出
,故FC垂直BD,有BEFC四点共圆而且FC为直径,由垂径定理可推出![]() ,进而可得BE=BC,再由30°直角三角形性质求出
,进而可得BE=BC,再由30°直角三角形性质求出![]() ,可得DE=BC,从而计算比值.
,可得DE=BC,从而计算比值.
解:(1)过E点作AB的垂线,垂足为G,交CD与H点,
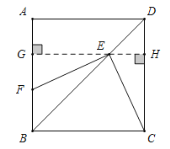
∴四边形DBCH为矩形,
∴BG=CH,
在矩形![]() 中,
中,![]() ,
,
∴矩形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() 和
和![]() 均为等腰直角三角形,即:GE=BE、DH=DH,
均为等腰直角三角形,即:GE=BE、DH=DH,
∴![]() ,
,
又∵![]() ,即
,即![]() ,
,
在![]() 中,
中,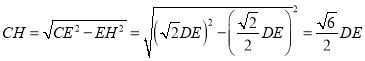 ,
,
∴ ,
,
在矩形BCHG中,HC=GB,
∴GE=HC,
又∵∠FEC=∠BGE=∠CHE=90°,
∴∠FEG=∠ECH
∴![]() (ASA)
(ASA)
∴FG=EH,
∴![]() ,
,
∴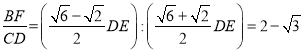
(2)以CF为直径作圆,
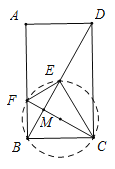
∵![]() 、∠ABC=90°,
、∠ABC=90°,
∴B、E在圆上,
又∵![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() ,
,
又∵FC是直径,
∴CF垂直平分BE,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为:(1)![]() ;(2)1.
;(2)1.

 阅读快车系列答案
阅读快车系列答案【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时,经历以下几个学习过程:
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
(2)描点并画出函数图象草图(在备用图1中描点并画图)

(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到?
答:______.
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F,E(-1,8),F(5,8),则不等式|x2-4x+3|>8的解集是______;
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点,求此时m的值.
【题目】为了估计某地区供暖期间空气质量情况,某同学在20天里做了如下记录:
污染指数(ω) | 40 | 60 | 80 | 100 | 120 | 140 |
天数(天) | 3 | 2 | 3 | 4 | 5 | 3 |
其中ω<50时空气质量为优,50≤ω≤100时空气质量为良,100<ω≤150时空气质量为轻度污染.若按供暖期125天计算,请你估计该地区在供暖期间空气质量达到良以上(含良)的天数为( )
A.75B.65C.85D.100