题目内容
【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时,经历以下几个学习过程:
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
(2)描点并画出函数图象草图(在备用图1中描点并画图)

(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到?
答:______.
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F,E(-1,8),F(5,8),则不等式|x2-4x+3|>8的解集是______;
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点,求此时m的值.
【答案】1.列表(完成表格)见解析;2.描点并画图见解析;3.(1)将函数![]() 的图像在x轴下方的部分关于x轴对称,在x轴上方的图像保持不变而得到函数y的图像;(2)
的图像在x轴下方的部分关于x轴对称,在x轴上方的图像保持不变而得到函数y的图像;(2)![]() 或
或![]() ;(3)①
;(3)①![]() ;②探究应用:
;②探究应用: ![]() 或
或![]() .
.
【解析】
(1)直接代入x值即可;
(2)描点并画图即可;
(3)(ⅰ)观察函数图像可得结果;
(ⅱ)观察图象直接求解不等式;
(ⅲ)①用待定系数法求出直线BC的解析式即可;
②画出函数图象,通过观察可知,m=0时就有三个交点;当直线平移时发现,直线与二次函数有两个相同交点时是三个交点变化的临界值,因此求这个值即可.
解:1.列表(完成表格)
| … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … | 15 | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15 | … |
| … | 15 | 8 | 3 | 0 | 1 | 0 | 3 | 8 | 15 | … |
2.描点并画图:

3.(1)观察图像函数将函数![]() 的图像在x轴下方的部分关于x轴对称,在x轴上方的图像保持不变而得到函数y的图像;
的图像在x轴下方的部分关于x轴对称,在x轴上方的图像保持不变而得到函数y的图像;
(2)不等式![]() 的解集是
的解集是 ![]() 或
或![]() ;
;
(3)①B(3,0),C(0,3),设直线BC的解析式为:y=kx+3,
则3k+3=0,解得:k=-1,
∴直线BC的解析式为:y=-x+3;
②(i)
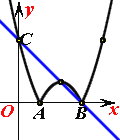
如上图,直线![]() 与
与![]() 的图象只有3个交点,此时,
的图象只有3个交点,此时,![]() ;
;
(ii)
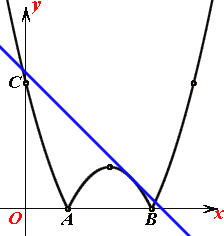
如上图,当直线![]() 与
与![]() 的图象只有3个交点,
的图象只有3个交点,
此时,![]()
消去y,整理得:![]() ,
,
该方程有两个相等的实数根,
![]()
解之,得:![]()
∴![]()
综上所述,![]() 或
或![]()

 每课必练系列答案
每课必练系列答案【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.