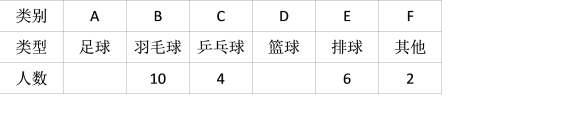ƒøƒ⁄»ð
°æƒø°øƒ≥𧓒∆∑µÍπ∫Ω¯A£¨B¡Ω÷÷𧓒∆∑£¨“—÷™’‚¡Ω÷÷𧓒∆∑µƒµ•º€÷Æ∫ÕŒ™200‘™£¨π∫Ω¯2∏ˆA÷÷𧓒∆∑∫Õ3∏ˆB÷÷𧓒∆∑–˪®∑—520‘™£Æ
£®1£©«ÛA£¨B¡Ω÷÷𧓒∆∑µƒµ•º€£ª
£®2£©∏√µÍ÷˜”˚”√9600‘™”√”⁄Ω¯ªı£¨«“◊Ó∂ýπ∫Ω¯A÷÷𧓒∆∑36∏ˆ£¨B÷÷𧓒∆∑µƒ ˝¡ø≤ª≥¨π˝A÷÷𧓒∆∑µƒ2±∂£¨‘Úπ≤”–º∏÷÷Ω¯ªı∑Ω∞∏£ø
£®3£©“—÷™ €≥ˆ“ª∏ˆA÷÷𧓒∆∑ø…ªÒ¿˚10‘™£¨ €≥ˆ“ª∏ˆB÷÷𧓒∆∑ø…ªÒ¿˚18‘™£¨∏√µÍ÷˜æˆ∂®√ø €≥ˆ“ª∏ˆB÷÷𧓒∆∑£¨Œ™œ£Õ˚π§≥ÃæËøÓm‘™£¨‘⁄£®2£©µƒÃıº˛œ¬£¨»ÙA£¨B¡Ω÷÷𧓒∆∑»´≤ø €≥ˆ∫ÛÀ˘”–∑Ω∞∏ªÒ¿˚æ˘œýÕ¨£¨‘Úmµƒ÷µ «∂ý…Ÿ£ø¥À ±µÍ÷˜ø…ªÒ¿˚∂ý…Ÿ‘™£ø
°æ¥∞∏°ø£®1£©A÷÷𧓒∆∑µƒµ•º€Œ™80‘™/∏ˆ£¨B÷÷𧓒∆∑µƒµ•º€Œ™120‘™/∏ˆ£ª£®2£©π≤”–7÷÷Ω¯ªı∑Ω∞∏£ª£®3£©mµƒ÷µ «3£¨¥À ±µÍ÷˜ø…ªÒ¿˚1200‘™£Æ
°æΩ‚Œˆ°ø
£®1£©…ËA÷÷𧓒∆∑µƒµ•º€Œ™x‘™/∏ˆ£¨B÷÷𧓒∆∑µƒµ•º€Œ™y‘™/∏ˆ£¨∏˘æð°∞A£¨B¡Ω÷÷𧓒∆∑µƒµ•º€÷Æ∫ÕŒ™200‘™£¨π∫Ω¯2∏ˆA÷÷𧓒∆∑∫Õ3∏ˆB÷÷𧓒∆∑–˪®∑—520‘™°±£¨º¥ø…µ√≥ˆπÿ”⁄x£¨yµƒ∂˛‘™“ª¥Œ∑Ω≥Ã◊È£¨Ω‚÷ƺ¥ø…µ√≥ˆΩ·¬€£ª
£®2£©…Ëπ∫Ω¯A÷÷𧓒∆∑a∏ˆ£¨‘Úπ∫Ω¯B÷÷𧓒∆∑![]() ∏ˆ£¨∏˘æð◊Ó∂ýπ∫Ω¯A÷÷𧓒∆∑36∏ˆ«“B÷÷𧓒∆∑µƒ ˝¡ø≤ª≥¨π˝A÷÷𧓒∆∑µƒ2±∂£¨º¥ø…µ√≥ˆπÿ”⁄aµƒ“ª‘™“ª¥Œ≤ªµ» Ω◊È£¨Ω‚÷ƺ¥ø…µ√≥ˆaµƒ»°÷µ∑∂Œß£¨‘ŸΩ·∫œaŒ™’˝’˚ ˝£¨º¥ø…µ√≥ˆΩ¯ªı∑Ω∞∏µƒ∏ˆ ˝£ª
∏ˆ£¨∏˘æð◊Ó∂ýπ∫Ω¯A÷÷𧓒∆∑36∏ˆ«“B÷÷𧓒∆∑µƒ ˝¡ø≤ª≥¨π˝A÷÷𧓒∆∑µƒ2±∂£¨º¥ø…µ√≥ˆπÿ”⁄aµƒ“ª‘™“ª¥Œ≤ªµ» Ω◊È£¨Ω‚÷ƺ¥ø…µ√≥ˆaµƒ»°÷µ∑∂Œß£¨‘ŸΩ·∫œaŒ™’˝’˚ ˝£¨º¥ø…µ√≥ˆΩ¯ªı∑Ω∞∏µƒ∏ˆ ˝£ª
£®3£©…Ë◊п˚»ÛŒ™w‘™£¨∏˘æð◊п˚»Û=µ•∏ˆ¿˚»Û°¡œ˙ € ˝¡ø£¨º¥ø…µ√≥ˆwπÿ”⁄aµƒ∫Ø ˝πÿœµ Ω£¨”…w÷µ”Îa÷µŒÞπÿø…µ√≥ˆmµƒ÷µ£¨‘Ÿ¥˙»Îm÷µº¥ø…«Û≥ˆwµƒ÷µ£Æ
£®1£©…ËA÷÷𧓒∆∑µƒµ•º€Œ™x‘™/∏ˆ£¨B÷÷𧓒∆∑µƒµ•º€Œ™y‘™/∏ˆ£¨
“¿Ã‚“‚£¨µ√£∫![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨
¥£∫A÷÷𧓒∆∑µƒµ•º€Œ™80‘™/∏ˆ£¨B÷÷𧓒∆∑µƒµ•º€Œ™120‘™/∏ˆ£ª
£®2£©…Ëπ∫Ω¯A÷÷𧓒∆∑a∏ˆ£¨‘Úπ∫Ω¯B÷÷𧓒∆∑![]() ∏ˆ£¨
∏ˆ£¨
“¿Ã‚“‚£¨µ√£∫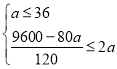 £¨
£¨
Ω‚µ√£∫30°Ða°Ð36£¨
°þaŒ™’˝’˚ ˝£¨
°ýπ≤”–7÷÷Ω¯ªı∑Ω∞∏£ª
£®3£©…Ë◊п˚»ÛŒ™w‘™£¨
“¿Ã‚“‚£¨µ√£∫w£Ω10a+£®18©Åm£©°¡![]() £Ω£®
£Ω£®![]() m©Å2£©a+1440©Å80m£¨
m©Å2£©a+1440©Å80m£¨
°þwµƒ÷µ”Îa÷µŒÞπÿ£¨
°ý![]() m©Å2£Ω0£¨
m©Å2£Ω0£¨
°ým£Ω3£¨¥À ±w£Ω1440©Å80m£Ω1200£¨
¥£∫mµƒ÷µ «3£¨¥À ±µÍ÷˜ø…ªÒ¿˚1200‘™£Æ

 ÷«ª€øŒÃ√√ÐæÌ100∑÷µ•‘™π˝πÿºÏ≤‚œµ¡–¥∞∏
÷«ª€øŒÃ√√ÐæÌ100∑÷µ•‘™π˝πÿºÏ≤‚œµ¡–¥∞∏ µ•‘™∆⁄÷–∆⁄ƒ©æÌœµ¡–¥∞∏
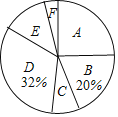
µ•‘™∆⁄÷–∆⁄ƒ©æÌœµ¡–¥∞∏°æƒø°øŒ™Ã·…˝—ß…˙µƒ“’ ıÀÿ—¯£¨ƒ≥–£º∆ªÆø™…ËÀƒ√≈—°–ÞøŒ≥ã∫…˘¿÷°¢ŒËµ∏°¢ È∑®°¢…„”∞£Æ“™«Û√ø√˚—ß…˙±ÿ–Η°–Þ«“÷ªƒÐ—°–Þ“ª√≈øŒ≥㨌™±£÷§º∆ªÆµƒ”––ß µ ©£¨—ß–£Àʪ˙∂‘≤ø∑÷—ß…˙Ω¯––¡À“ª¥Œµ˜≤È£¨≤¢Ω´µ˜ñÀΩ·π˚ªÊ÷∆≥…»Áœ¬≤ªÕÍ’˚µƒÕ≥º∆±Ì∫ÕÕ≥º∆Õº£Æ
—ß…˙—°–ÞøŒ≥ÃÕ≥º∆±Ì
øŒ≥à | »À ˝ | À˘’º∞Ÿ∑÷±» |
…˘¿÷ | 14 |
|
ŒËµ∏ | 8 |
|
鷨 | 16 |
|
…„”∞ |
|
|
∫œº∆ |
|
|

∏˘æð“‘…œ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©![]() °°°°£¨
°°°°£¨![]() °°°°£Æ
°°°°£Æ
£®2£©«Û≥ˆ![]() µƒ÷µ≤¢≤π»´Ãı–ŒÕ≥º∆Õº£Æ
µƒ÷µ≤¢≤π»´Ãı–ŒÕ≥º∆Õº£Æ
£®3£©∏√–£”–1500√˚—ß…˙£¨«Îƒ„π¿º∆—°–Þ°∞…˘¿÷°±øŒ≥õƒ—ß…˙”–∂ý…Ÿ√˚£Æ
£®4£©∆þ£®1£©∞ý∫Õ∆þ£®2£©∞ý∏˜”–2»À—°–Þ°∞ŒËµ∏°±øŒ≥ë“”–ŒËµ∏ª˘¥°£¨—ß–£◊º±∏¥”’‚4»À÷–Àʪ˙≥È»°2»À±ý≈≈°∞ŒËµ∏°±‘⁄ø™∞ý“« Ω…œ±Ì—𣨫Δ√¡–±Ì∑®ªÚª≠ ˜◊¥Õºµƒ∑Ω∑®«ÛÀ˘≥È»°µƒ2»À«°∫√¿¥◊‘Õ¨“ª∏ˆ∞ýº∂µƒ∏≈¬ £Æ
°æƒø°øƒ≥–£…Ë”–Ô˝—°–ÞøŒ£¨√øŒªÕ¨—ß±ÿ–Î¥””√´«Ú°¢¿∫«Ú°¢∆π≈“«Ú°¢≈≈«Ú°¢◊„«ÚŒÂœÓ«Ú¿ý‘À∂Ø÷– —°‘Ò“ªœÓ«“÷ªƒÐ—°‘Ò“ªœÓ«Ú¿ý‘À∂Ø£¨‘⁄∏√–£—ß…˙÷–Àʪ˙≥È»°10% µƒ—ß…˙Ω¯––µ˜≤È£¨∏˘æðµ˜≤È Ω·π˚ªÊ÷∆≥…»ÁÕºÀ˘ 浃…–≤ªÕÍ’˚µƒ∆µ ˝∑÷≤º±Ì∫Õ…»–ŒÕ≥º∆Õº£Æ
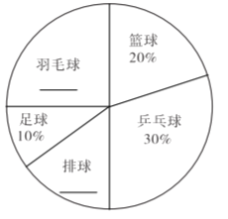
‘À∂؜Ӄø | ∆µ ˝ |
”√´«Ú |
|
¿∫«Ú |
|
±¯≈“«Ú |
|
≈≈«Ú |
|
◊„«Ú |
|
«Î∏˘æð“‘…œÕº°¢±Ì–≈œ¢Ω‚¥œ¬¡–Œ Â:
£®1£©∆µ ˝∑÷≤º±Ì÷–µƒ![]() £¨
£¨![]() £ª
£ª
£®2£©≤π»´…»–ŒÕ≥º∆Õº£ª
£®3£©≈≈«ÚÀ˘‘⁄µƒ…»–Œµƒ‘≤–ƒΩ«Œ™ ∂»£ª
£®4£©»´–£”–∂ý…Ÿ√˚—ß…˙—°‘Ò≤Œº”∆π≈“«Ú‘À∂Ø?