题目内容
【题目】在国家政策的宏观调控下，某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4，5两月平均每月降价的百分率约是多少？(参考数据：
≈0.95)
(2)如果房价继续跌落，按此降价的百分率，你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2？请说明理由．
【答案】（1）4，5两月平均每月降价的百分率约为5%；（2）7月份该市的商品房成交均价不会跌破10 000元/m2
【解析】
（1）设4、5两月平均每月降价的百分率是x，那么4月份的房价为14000（1x），5月份的房价为
，然后根据5月份的12600元/ m2即可列出方程解决问题；
（2）根据（1）的结果可以计算出7月份商品房成交均价，然后和10000元/m2进行比较即可作出判断．
解：(1)设平均每月降价的百分率为x，依题意得
14000(1－x)2＝12600，
(1－x)2＝0.9，
解得x1≈0.05，x2≈1.95(不合题意，舍去)，
则4，5两月平均每月降价的百分率约为5%
(2)12600(1－x)2＝12600×0.9＝11340>10000，
故7月份该市的商品房成交均价不会跌破10000元/m2
【题目】某厂按用户的月需求量
（件）完成一种产品的生产，其中
.每件的售价为18万元，每件的成本
（万元）是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量（件）成反比.经市场调研发现，月需求量与月份
（为整数，
）符合关系式
（
为常数），且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
（1）求与满足的关系式，请说明一件产品的利润能否是12万元；
（2）求，并推断是否存在某个月既无盈利也不亏损；
（3）在这一年12个月中，若第
个月和第
个月的利润相差最大，求
.
【题目】某公司经销的一种产品每件成本为40元，要求在90天内完成销售任务．已知该产品90天内每天的销售价格与时间（第x天）的关系如下表：
时间（第x天） | 1≤x＜50 | 50≤x≤90 |
x+50 | 90 |
任务完成后，统计发现销售员小王90天内日销售量p（件）与时间（第x天）满足一次函数关系p＝﹣2x+200．设小王第x天销售利润为W元．
（1）直接写出W与x之间的函数关系式，井注明自变量x的取值范围；
（2）求小生第几天的销售量最大？最大利润是多少？
（3）任务完成后，统计发现平均每个销售员每天销售利润为4800公司制定如下奖励制度：如果一个销售员某天的销售利润超过该平均值，则该销售员当天可获得200元奖金．请计算小王一共可获得多少元奖金？
【题目】某校设有体育选修课，每位同学必须从羽毛球、篮球、乒乓球、排球、足球五项球类运动中 选择一项且只能选择一项球类运动，在该校学生中随机抽取10% 的学生进行调查，根据调查 结果绘制成如图所示的尚不完整的频数分布表和扇形统计图．
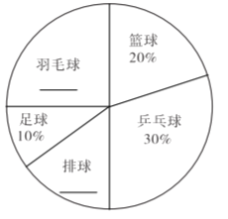
运动项目 | 频数 |
羽毛球 |
|
篮球 |
|
兵乓球 |
|
排球 |
|
足球 |
|
请根据以上图、表信息解答下列问题:
（1）频数分布表中的
，
；
（2）补全扇形统计图；
（3）排球所在的扇形的圆心角为 度；
（4）全校有多少名学生选择参加乒乓球运动?
