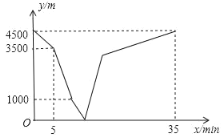
题目内容
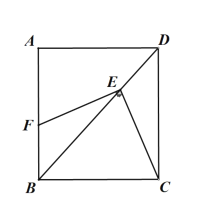
【题目】己知，在矩形
中，点
为
的中点，点
为
上一点，连接
、
，若
，
，
，则线段的长为_________．
【答案】
或
【解析】
根据点F靠近点A和点F靠近点B分类讨论，分别画出对应的图形，根据矩形的判定及性质、勾股定理、垂直平分线的性质即可分别求出结论．
解：①当点F靠近点A时，如下图所示，过点F作FG⊥DC于G
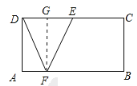
易知四边形ABCD、DAFG和GFBC都为矩形
∴GF=BC=2，CD=AB=4
在Rt△GEF中，EG=
∵点
为
的中点，
∴DE=
=2
∴DE=2EG
即点G为DE的中点
∴FG垂直平分DE
∴DF=EF=；
②当点F靠近点B时，如下图所示过点F作FG⊥DC于G
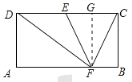
易知四边形ABCD、DAFG和GFBC都为矩形
∴GF=BC=2，CD=AB=4
在Rt△GEF中，EG=
∵点为的中点，
∴DE==2
∴DG=DE＋EG=3
在Rt△DFG中，DF=
综上：DF=或
故答案为：或．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
