题目内容
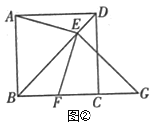
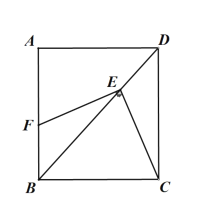
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,动点
中,动点![]() 分别以相同的速度从
分别以相同的速度从![]() 两点同时出发向点
两点同时出发向点![]() 和点
和点![]() 运动(任何一个点到达即停止),连接
运动(任何一个点到达即停止),连接![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则线段
,则线段![]() 的最小值为________.
的最小值为________.
【答案】![]()
【解析】
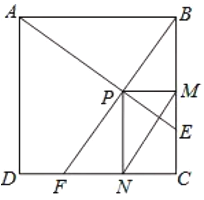
由正方形的性质及条件可证明△ABE≌△BCF,即可得∠BAE=∠CBF,再根据∠BAE+∠BEA=90°,可得∠CBF+∠BEA=90°,可得出∠APB=90°,进而得到点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,最后在Rt△BCG中,根据勾股定理,求出CG的长度,再求出PG的长度,即可求出线段CP的最小值,即可得到线段![]() 的最小值.
的最小值.
解:∵动点F,E的速度相同,
∴DF=CE,
又∵CD=BC,
∴CF=BE,
又∵AB=BC,∠ABE=∠BCF=90°,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠APB=90°,
∴点P的路径是一段以AB为直径的弧,
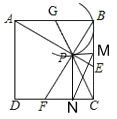
设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,
在Rt△BCG中,CG=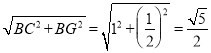 ,
,
∵PG=![]() AB=
AB=![]() ,
,
∴CP=CGPG=![]() ,
,
易得四边形NCMP是矩形,
∴MN=CP,
∴线段MN的最小值为![]()
故答案为:![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某家庭记录了未使用节水龙头50天的日用水量(单位:m3)和使用了节木龙头50天的日用水量,得到频数分布表如下:
表1未使用节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 | 0.6≤x≤0.7 |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
表2使用了节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)估计该家庭使用节水龙头后,日用水量小于0.3 m3的概率;
(2)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在范围的组中值作代表.)
【题目】为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调査结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|

根据以上信息,解答下列问题:
(1)![]() ,
,![]() .
.
(2)求出![]() 的值并补全条形统计图.
的值并补全条形统计图.
(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.
【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.