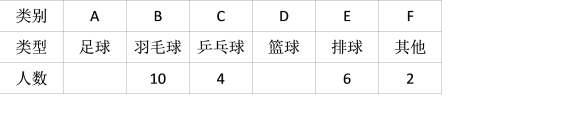题目内容
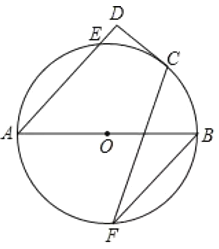
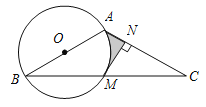
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,图中阴影部分的面积为( )
,图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
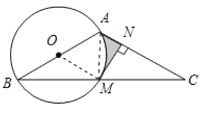
先证明MN为⊙O切线,求阴影部分的面积要把它转化成S梯形ANMOS扇形OAM,再分别求的这两部分的面积求解.
证明:连接OM.
∵OM=OB,
∴∠B=∠OMB.
∵AB=AC,
∴∠B=∠C.
∴∠OMB=∠C.
∴OM∥AC.
∵MN⊥AC,
∴OM⊥MN.
∵点M在⊙O上,
∴MN是⊙O的切线;
连接AM.
∵AB为直径,点M在⊙O上,
∴∠AMB=90![]() .
.
∵AB=AC,∠BAC=120![]() ,
,
∴∠B=∠C=30![]() .
.
∴∠AOM=60![]() .
.
又∵在Rt△AMC中,MN⊥AC于点N,
∴∠AMN=30![]() .
.
∴AN=AMsin∠AMN=ACsin30![]() sin30
sin30![]() =
=![]() .
.
∴MN=AMcos∠AMN=ACsin30![]() cos30
cos30![]() =
=![]() .
.
∴S梯形ANMO=![]() (AN+OM)MN=
(AN+OM)MN=![]() ,
,
S扇形OAM=![]() =
=![]() ,
,
∴S阴影=S梯形ANMOS扇形OAM=![]() .
.
故选:B.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案【题目】某公司经销的一种产品每件成本为40元,要求在90天内完成销售任务.已知该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
x+50 | 90 |
任务完成后,统计发现销售员小王90天内日销售量p(件)与时间(第x天)满足一次函数关系p=﹣2x+200.设小王第x天销售利润为W元.
(1)直接写出W与x之间的函数关系式,井注明自变量x的取值范围;
(2)求小生第几天的销售量最大?最大利润是多少?
(3)任务完成后,统计发现平均每个销售员每天销售利润为4800公司制定如下奖励制度:如果一个销售员某天的销售利润超过该平均值,则该销售员当天可获得200元奖金.请计算小王一共可获得多少元奖金?
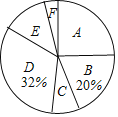
【题目】某校设有体育选修课,每位同学必须从羽毛球、篮球、乒乓球、排球、足球五项球类运动中 选择一项且只能选择一项球类运动,在该校学生中随机抽取10% 的学生进行调查,根据调查 结果绘制成如图所示的尚不完整的频数分布表和扇形统计图.
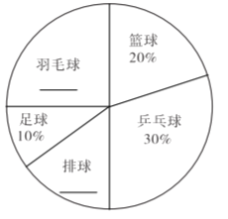
运动项目 | 频数 |
羽毛球 |
|
篮球 |
|
兵乓球 |
|
排球 |
|
足球 |
|
请根据以上图、表信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)补全扇形统计图;
(3)排球所在的扇形的圆心角为 度;
(4)全校有多少名学生选择参加乒乓球运动?