题目内容
【题目】如图，将斜边长为4的直角三角板放在直角坐标系xOy中，两条直角边分别与坐标轴重合，P为斜边的中点．现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是（ ）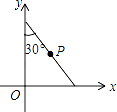
A.（ 
，1）
B.（1，﹣ ）
C.（2 ，﹣2）
D.（2，﹣2 ）
【答案】B
【解析】如图连接OP，因为
AOB=90°，OAB=30°，
则ABO=60°，
因为P是AB的中点，
所以OP=
AB=2，且OP=PB，
则三角形OPB是等边三角形，
所以∠POB=60°，
因为现将此三角板绕点O顺时针旋转120°，
则点P也绕点O顺时针旋转120°到P'
则COP'=POP'-POB=120°-60°=60°，
又因为OP=OP'，连接PP'交OB于C，则OPP'=OP'P=30°，则PP'
OB，则OC=OP'=1，CP'=
OP’=
,
则P'（1，
）.故选B.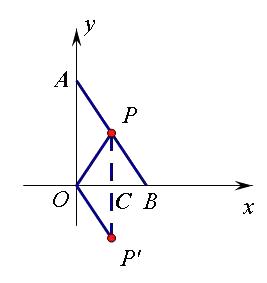
【考点精析】利用含30度角的直角三角形和直角三角形斜边上的中线对题目进行判断即可得到答案，需要熟知在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；直角三角形斜边上的中线等于斜边的一半．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
