Question

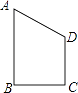
【题目】如图1，直角坐标系中有一矩形OABC，其中O是坐标原点，点A，C分别在x轴和y轴上，点B的坐标为（3，4），直线y= x交AB于点D，点P是直线y= x位于第一象限上的一点，连接PA，以PA为半径作⊙P，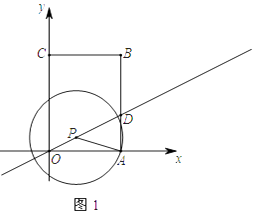
（1）连接AC，当点P落在AC上时，求PA的长；
（2）当⊙P经过点O时，求证：△PAD是等腰三角形；
（3）设点P的横坐标为m， ①在点P移动的过程中，当⊙P与矩形OABC某一边的交点恰为该边的中点时，求所有满足要求的m值；
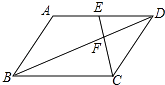
②如图2，记⊙P与直线y= x的两个交点分别为E，F（点E在点P左下方），当DE，DF满足 ＜ ＜3时，求m的取值范围．（请直接写出答案）

Answer 1

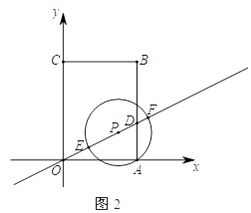
【答案】
（1）解：如图1中，

∵B（3，4）∴BC=3，AB=4

∵∠B=90°∴AC=5

∵OC∥AB，

∴△OPC∽△ADP，

∴ ，

即

∴ ．

（2）解：∵⊙P经过点O，

∴OP=AP

∴∠POA=∠PAO，

∵∠PDA+∠POA=∠DAP+∠PAO，

∴∠PDA=∠DAP，

∴△PAD是等腰三角形．

（3）解：①分4种情形讨论：

ⅰ）如图2中，

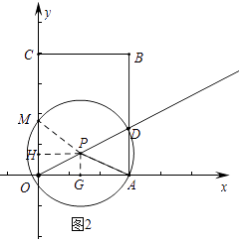
交点M是OC中点，PM=PA

则 ，

解得 ．

ⅱ）如图3中，

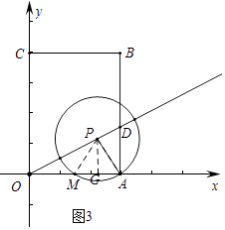
交点M是OA中点，PM=PA

∴MG=GA= ，

∴ ．

ⅲ）如图4中，

交点M是AB中点，PM=PA

∴PG= AM=1，

∴PH=2DH=2× =1，

∴m=2．

ⅳ）如图5中，

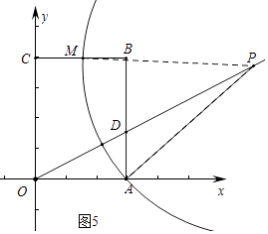
交点M是BC中点，PM=PA

则 ，

解得 ．

综上所述，满足要求的m值为 或 或2或 ．

②如图6中，当DE=3DF时，易知PA=2PD．

设P（m， ），则 =2 ，

解得m= 或4，

当m=4时，ED= DF，

综上可知，当DE，DF满足 ＜ ＜3时，m的取值范围为 ＜m＜4．

【解析】（1）由△OPC∽△ADP，可得 ，求出AC、AD即可解决问题；（2）只要证明∠PDA=∠DAP即可．（3）①分三种情形分别求解即可ⅰ）如图2中，交点M是OC中点，PM=PA；ⅱ）如图3中，交点M是OA中点，PM=PA；ⅲ）如图4中，交点M是AB中点，PM=PA；ⅳ）如图5中，交点M是BC中点，PM=PA；②如图6中，当DE=3DF时，易知PA=2PD．由此列出方程即可解决问题．