题目内容
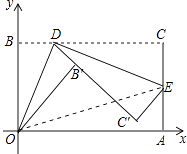
【题目】如图,Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C,D分别是BO,BA的中点,点E在CD的延长线上.若函数y1= ![]() (x>0)的图象经过B,E,函数y2=
(x>0)的图象经过B,E,函数y2= ![]() (x>0)的图象过点C,且△BCE的面积为1,则k2的值为( )
(x>0)的图象过点C,且△BCE的面积为1,则k2的值为( ) 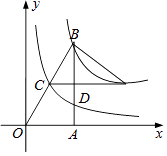
A.![]()
B.![]()
C.3
D.![]()
【答案】B
【解析】解:∵点C为线段OB的中点,且函数y1= ![]() (x>0)的图象经过B,E,函数y2=
(x>0)的图象经过B,E,函数y2= ![]() (x>0)的图象过点C, ∴k1=4k2 .
(x>0)的图象过点C, ∴k1=4k2 .
设点C的坐标为(m, ![]() )(m>0),则点B的坐标为(2m,
)(m>0),则点B的坐标为(2m, ![]() ),点E的坐标为(4m,
),点E的坐标为(4m, ![]() ),
),
∴CE=3m,BD= ![]() ,
,
∴S△BCE= ![]() CEBD=
CEBD= ![]() ×3m×
×3m× ![]() =
= ![]() k2=1,
k2=1,
解得:k2= ![]() .
.
故选B.
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目