题目内容
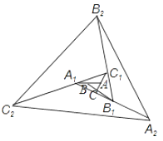
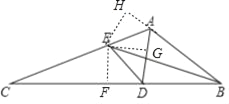
【题目】如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.

【答案】(1)见解析;(2)30°.
【解析】
(1)过E作EH⊥AB于H,EF⊥BC于F,EG⊥AD于G,
∵AD平分∠BAC,∠BAC=120°,
∴∠BAD=∠CAD=60°,
∵∠CAH=180°﹣120°=60°,
∴AE平分∠HAD,
∴EH=EG,
∵BE平分∠ABC,EH⊥AB,EF⊥BC,
∴EH=EF,
∴EF=EG,
∴点E到DA、DC的距离相等;
(2)解:∵由(1)知:DE平分∠ADC,
∴∠EDC=∠DEB+∠DBE,
∴![]() =∠DEB+
=∠DEB+![]() ∠ABC,
∠ABC,
∴∠DEB=![]() (∠CDA﹣∠ABC)=
(∠CDA﹣∠ABC)=![]() ∠BAD=30°.
∠BAD=30°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目