题目内容
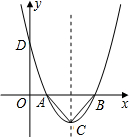
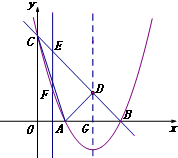
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴相交于点C.连接AC,BC,A(-3,0),C(0,
),且当x=-4和x=2时二次函数的函数值y相等.
(1)求抛物线的解析式;
(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.
①当运动时间为t秒时,连接MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,求t的值及点P的坐标;
②抛物线的对称轴上是否存在点Q,使得以B、N、Q为顶点的三角形与△A0C相似?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
③当运动时间为t秒时,连接MN,将△BMN沿MN翻折,得到△PMN.并记△PMN与△AOC的重叠部分的面积为S.求S与t的函数关系式.

| 3 |
(1)求抛物线的解析式;
(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.
①当运动时间为t秒时,连接MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,求t的值及点P的坐标;
②抛物线的对称轴上是否存在点Q,使得以B、N、Q为顶点的三角形与△A0C相似?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
③当运动时间为t秒时,连接MN,将△BMN沿MN翻折,得到△PMN.并记△PMN与△AOC的重叠部分的面积为S.求S与t的函数关系式.

(1)∵当x=-4和x=2时二次函数的函数值y相等,
∴抛物线对称轴:x=-
=-1,即b=2a;
由C(0,
)得:c=
;
将A(-3,0)代入y=ax2+2ax+
(a≠0)中,得:
9a-6a+
=0,a=-
∴抛物线的解析式:y=-
x2-
x+
.
(2)由(1)的抛物线解析式知:A(-3,0)、B(1,0)、C(0,
),则:
OA=3,OB=1,OC=
,即 OC2=OA•OB,又OC⊥AB,则△ABC是直角三角形,且∠CAB=30°,∠ABC=60°;
①△BMN中,BM=BN=t,∠NBM=60°,即△BNM是等边三角形;
由于△PMN由△BMNA翻转所得,所以△PMN也是等边三角形,四边形PNBM是菱形;
∴PN∥AB(如题干图),得:
=
,代入数据,有:
=
,解得:t=
;
由tan∠CAO=
、C(0,
)得,直线AC:y=
x+
;
当y=t•sin60°=
时,
x+
=
,x=-1
即 P(-1,
);
综上,B点恰好落在AC边上的P处时,t=
,P(-1,
).
②∵△AOC是一个含30°角的直角三角形,
∴若以B、N、Q为顶点的三角形与△A0C相似,那么△BNQ也必须是一个含30°角的直角三角形.
分三种情况讨论:
Ⅰ、∠QNB=90°、∠BQN=30°(如②-Ⅰ图);
∵∠ABC=∠Q1BN=60°,∴点Q1在x轴上,即Q1(-1,0);
Ⅱ、∠QBN=90°、∠BQN=30°(如②-Ⅱ图);
此时BQ2∥AC,设直线BQ2:y=
x+b,代入B(1,0),得:b=-
∴直线BQ2:y=
x-
,Q2(-1,-
);
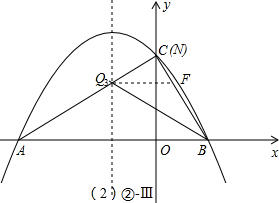
Ⅲ、∠QNB=90°、∠QBN=30°(如②-Ⅲ图);
此时N、C重合,点Q3应在①的P点处,由①的计算结果知:
Q3C=
•sin60°=
,而BC=2,即∠CQ3B=60°,符合条件;
即 Q3(-1,
);
综上,符合条件的Q点的坐标为:Q1(-1,0)、Q2(-1,-
)、Q3(-1,
).
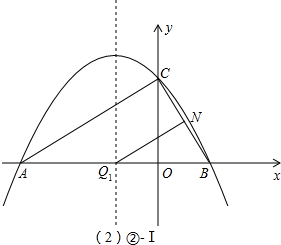

③当点P落在y轴上时,
=
,即
=
,解得:t=
;
当点M、O重合时,t=OB=1;
当点P落在AC上时,由①知,t=
;
Ⅰ、当0<t≤
时,△PMN和△AOC不重合,即S=0;
Ⅱ、当
<t≤1时(如③-Ⅱ图),由
=
可求得:GN=1-
,PG=PN-GN=t-(1-
)=
-1;
S=S△PGH=
×(
-1)×(
-1)
=
(
-1)2;
Ⅲ、当1<t≤
时(如③-Ⅲ图);
由Ⅱ知,GN=1-
,GH=
GN=
∴抛物线对称轴:x=-
| b |
| 2a |
由C(0,
| 3 |
| 3 |
将A(-3,0)代入y=ax2+2ax+
| 3 |
9a-6a+
| 3 |
| ||
| 3 |
∴抛物线的解析式:y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(2)由(1)的抛物线解析式知:A(-3,0)、B(1,0)、C(0,
| 3 |
OA=3,OB=1,OC=
| 3 |
①△BMN中,BM=BN=t,∠NBM=60°,即△BNM是等边三角形;
由于△PMN由△BMNA翻转所得,所以△PMN也是等边三角形,四边形PNBM是菱形;
∴PN∥AB(如题干图),得:
| PN |
| AB |
| CN |
| BC |
| t |
| 4 |
| 2-t |
| 2 |
| 4 |
| 3 |
由tan∠CAO=
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
当y=t•sin60°=
2
| ||
| 3 |
| ||
| 3 |
| 3 |
2
| ||
| 3 |
即 P(-1,
2
| ||
| 3 |
综上,B点恰好落在AC边上的P处时,t=
| 4 |
| 3 |
2
| ||
| 3 |
②∵△AOC是一个含30°角的直角三角形,
∴若以B、N、Q为顶点的三角形与△A0C相似,那么△BNQ也必须是一个含30°角的直角三角形.
分三种情况讨论:
Ⅰ、∠QNB=90°、∠BQN=30°(如②-Ⅰ图);
∵∠ABC=∠Q1BN=60°,∴点Q1在x轴上,即Q1(-1,0);
Ⅱ、∠QBN=90°、∠BQN=30°(如②-Ⅱ图);
此时BQ2∥AC,设直线BQ2:y=
| ||
| 3 |
| ||
| 3 |
∴直线BQ2:y=
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
Ⅲ、∠QNB=90°、∠QBN=30°(如②-Ⅲ图);
此时N、C重合,点Q3应在①的P点处,由①的计算结果知:
Q3C=
| 4 |
| 3 |
2
| ||
| 3 |
即 Q3(-1,
2
| ||
| 3 |
综上,符合条件的Q点的坐标为:Q1(-1,0)、Q2(-1,-
2
| ||
| 3 |
2
| ||
| 3 |
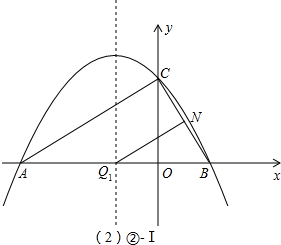


③当点P落在y轴上时,
| PN |
| OB |
| CN |
| BC |
| t |
| 1 |
| 2-t |
| 2 |
| 2 |
| 3 |
当点M、O重合时,t=OB=1;
当点P落在AC上时,由①知,t=
| 4 |
| 3 |
Ⅰ、当0<t≤
| 2 |
| 3 |
Ⅱ、当
| 2 |
| 3 |
| GN |
| OB |
| CN |
| CB |
| t |
| 2 |
| t |
| 2 |
| 3t |
| 2 |
S=S△PGH=
| 1 |
| 2 |
| 3t |
| 2 |
| 3t |
| 2 |
| 3 |
| ||
| 2 |
| 3t |
| 2 |
Ⅲ、当1<t≤
| 4 |
| 3 |
由Ⅱ知,GN=1-
| t |
| 2 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案 天天向上一本好卷系列答案 小学生10分钟应用题系列答案 小学生10分钟应用题系列答案
相关题目
|
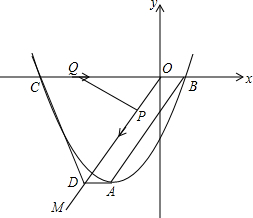

 、B两点.
、B两点.
