题目内容
已知矩形纸片OABC的长为4,宽为3,以长OA所在的直线为x轴,O为坐标原点建立平面直角坐标系;点P是OA边上的动点(与点O、A不重合),现将△POC沿PC翻折得到△PEC,再在AB边上选取适当的点D,将△PAD沿PD翻折,得到△PFD,使得直线PE、PF重合.
(1)若点E落在BC边上,如图①,求点P、C、D的坐标,并求过此三点的抛物线的函数关系式;
(2)若点E落在矩形纸片OABC的内部,如图②,设OP=x,AD=y,当x为何值时,y取得最大值?
(3)在(1)的情况下,过点P、C、D三点的抛物线上是否存在点Q,使△PDQ是以PD为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.

(1)若点E落在BC边上,如图①,求点P、C、D的坐标,并求过此三点的抛物线的函数关系式;
(2)若点E落在矩形纸片OABC的内部,如图②,设OP=x,AD=y,当x为何值时,y取得最大值?
(3)在(1)的情况下,过点P、C、D三点的抛物线上是否存在点Q,使△PDQ是以PD为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.

(1)由题意知,△POC,△PAD均为等腰直角三角形,可得P(3,0),C(0,3),D(4,1),
设过此三点的抛物线为y=ax2+bx+c(a≠0),
则
|
∴
|
∴过P、C、D三点的抛物线的函数关系式为y=
| 1 |
| 2 |
| 5 |
| 2 |
(2)由已知PC平分∠OPE,PD平分∠APF,且PE、PF重合,则∠CPD=90°,
∴∠OPC+∠APD=90°,又∠APD+∠ADP=90°,
∴∠OPC=∠ADP.
∴Rt△POC∽Rt△DAP.
∴
| OP |
| AD |
| OC |
| AP |
| x |
| y |
| 3 |
| 4-x |
∵y=
| 1 |
| 3 |
=-
| 1 |
| 3 |
| 4 |
| 3 |
=-
| 1 |
| 3 |
| 4 |
| 3 |
∴当x=2时,y有最大值
| 4 |
| 3 |
(3)假设存在,分两种情况讨论:
①当∠DPQ=90°时,由题意可知∠DPC=90°,且点C在抛物线上,
故点C与点Q重合,所求的点Q为(0,3)
②当∠QDP=90°时,过点D作平行于PC的直线DQ,假设直线DQ交抛物线于另-点Q,
∵点P(3,0),C(0,3),
∴直线PC的方程为y=-x+3,将直线PC向上平移2个单位与直线DQ重合,
∴直线DQ的方程为y=-x+5.
由
|
得
|
|
又点D(4,1),∴Q(-1,6),故该抛物线上存在两点Q(0,3),(-1,6)满足条件.



练习册系列答案
相关题目



 点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为______.
点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为______. 点B的左侧),与y轴交于点C.
点B的左侧),与y轴交于点C.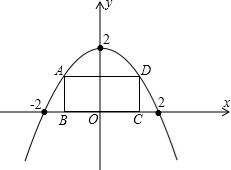 x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.