题目内容
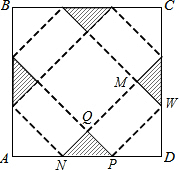
如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
(1)若折叠后长方体底面正方形的面积为1250cm2,求长方体包装盒的高;
(2)设剪掉的等腰直角三角形的直角边长为x(cm),长方体的侧面积为S(cm2),求S与x的函数关系式,并求x为何值时,S的值最大.

(1)若折叠后长方体底面正方形的面积为1250cm2,求长方体包装盒的高;
(2)设剪掉的等腰直角三角形的直角边长为x(cm),长方体的侧面积为S(cm2),求S与x的函数关系式,并求x为何值时,S的值最大.

(1)设剪掉阴影部分的每个等腰直角三角形的腰长为xcm,则NP=
xcm,
DP=
,QM=PW=
×
,
由题意得:(
×
)2=1250.
解得,x1=5
,x2=55
(超过60,故不符合题意舍去),
答:长方体包装盒的高为5
cm.
另法:∵由已知得底面正方形的边长为
=25
,
∴AN=25
×
=25.
∴PN=60-25×2=10.
∴PQ=10×
=5
(cm).
答:长方体包装盒的高为5
cm.
(2)由题意得,S=4×S四边形QPWM=4×PW•QP,
∵PW=
×
,QP=x,
∴S=4×
×
×x=-4x2+120
x.
∵a=-4<0,
∴当x=15
时,S有最大值.
| 2 |
DP=
60-
| ||
| 2 |
| 2 |
60-
| ||
| 2 |
由题意得:(
60-
| ||
| 2 |
| 2 |
解得,x1=5
| 2 |
| 2 |
答:长方体包装盒的高为5
| 2 |
另法:∵由已知得底面正方形的边长为
| 1250 |
| 2 |
∴AN=25
| 2 |
| ||
| 2 |
∴PN=60-25×2=10.
∴PQ=10×
| ||
| 2 |
| 2 |
答:长方体包装盒的高为5
| 2 |
(2)由题意得,S=4×S四边形QPWM=4×PW•QP,
∵PW=
| 2 |
60-
| ||
| 2 |
∴S=4×
| 2 |
60-
| ||
| 2 |
| 2 |
∵a=-4<0,
∴当x=15
| 2 |


练习册系列答案
相关题目


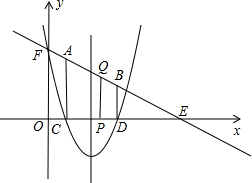 求四边形PQFC的面积S与t之间的函数关系式,并确定t的取值范围.
求四边形PQFC的面积S与t之间的函数关系式,并确定t的取值范围.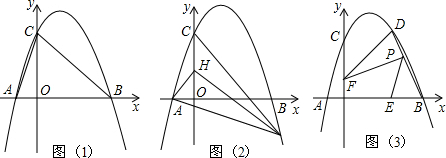
 点B的左侧),与y轴交于点C.
点B的左侧),与y轴交于点C.