题目内容
如图,顶点坐标为(2,-1)的抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),与x轴交于A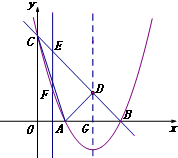 、B两点.
、B两点.
(1)求抛物线的表达式;
(2)设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,求点E的坐标;若不存在,请说明理由.
 、B两点.
、B两点.(1)求抛物线的表达式;
(2)设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,求点E的坐标;若不存在,请说明理由.
(1)依题意,设抛物线的解析式为 y=a(x-2)2-1,代入C(O,3)后,得:
a(0-2)2-1=3,a=1
∴抛物线的解析式:y=(x-2)2-1=x2-4x+3.
(2)由(1)知,A(1,0)、B(3,0);
设直线BC的解析式为:y=kx+3,代入点B的坐标后,得: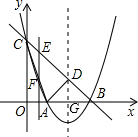
3k+3=0,k=-1
∴直线BC:y=-x+3;
由(1)知:抛物线的对称轴:x=2,则 D(2,1);
∴AD=
=
,AC=
=
,CD=
=2
,
即:AC2=AD2+CD2,△ACD是直角三角形,且AD⊥CD;
∴S△ACD=
AD•CD=
×
×2
=2.
(3)由题意知:EF∥y轴,则∠FED=∠OCB,若△OCB与△FED相似,则有:
①∠DFE=90°,即 DF∥x轴;
将点D纵坐标代入抛物线的解析式中,得:
x2-4x+3=1,解得 x=2±
;
当x=2+
时,y=-x+3=1-
;
当x=2-
时,y=-x+3=1+
;
∴E1(2+
,1-
)、E2(2-
,1+
).
②∠EDF=90°;
易知,直线AD:y=x-1,联立抛物线的解析式有:
x2-4x+3=x-1,
x2-5x+4=0,
解得 x1=1、x2=4;
当x=1时,y=-x+3=2;
当x=4时,y=-x+3=-1;
∴E3(1,2)、E4(4,-1).
综上,存在符合条件的点E,且坐标为:(2+
,1-
)、(2-
,1+
)、(1,2)或(4,-1).
a(0-2)2-1=3,a=1
∴抛物线的解析式:y=(x-2)2-1=x2-4x+3.
(2)由(1)知,A(1,0)、B(3,0);
设直线BC的解析式为:y=kx+3,代入点B的坐标后,得:

3k+3=0,k=-1
∴直线BC:y=-x+3;
由(1)知:抛物线的对称轴:x=2,则 D(2,1);
∴AD=
| AG2+DG2 |
| 2 |
| OC2+OA2 |
| 10 |
| (3-1)2+22 |
| 2 |
即:AC2=AD2+CD2,△ACD是直角三角形,且AD⊥CD;
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
(3)由题意知:EF∥y轴,则∠FED=∠OCB,若△OCB与△FED相似,则有:
①∠DFE=90°,即 DF∥x轴;
将点D纵坐标代入抛物线的解析式中,得:
x2-4x+3=1,解得 x=2±
| 2 |
当x=2+
| 2 |
| 2 |

当x=2-
| 2 |
| 2 |
∴E1(2+
| 2 |
| 2 |
| 2 |
| 2 |
②∠EDF=90°;
易知,直线AD:y=x-1,联立抛物线的解析式有:
x2-4x+3=x-1,
x2-5x+4=0,
解得 x1=1、x2=4;
当x=1时,y=-x+3=2;
当x=4时,y=-x+3=-1;
∴E3(1,2)、E4(4,-1).
综上,存在符合条件的点E,且坐标为:(2+
| 2 |
| 2 |
| 2 |
| 2 |

练习册系列答案
相关题目


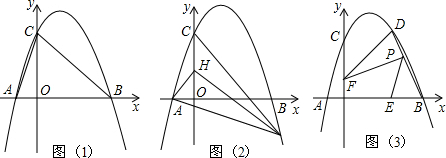
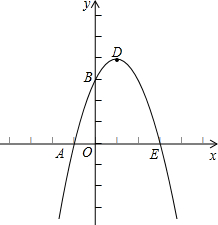

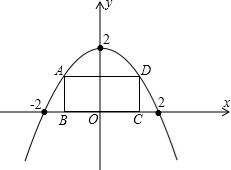 x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.