题目内容
已知二次函数y=
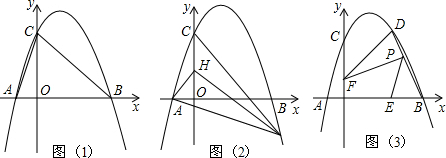
x2+bx+c的图象经过点A(-3,6),并且与x轴交于点B(-1,0)和点C,顶点为P.
(1)求这个二次函数解析式;
(2)设D为线段OC上的点,满足∠DPC=∠BAC,求点D的坐标.
| 1 |
| 2 |
(1)求这个二次函数解析式;
(2)设D为线段OC上的点,满足∠DPC=∠BAC,求点D的坐标.
(1)已知抛物线过A(-3,6),B(-1,0)则有:
解得
∴二次函数的解析式为:y=
x2-x-
;
(2)易知:P(1,-2),C(3,0),
过P作PM⊥x轴于M,
则PM=2,
∵抛物线过C(3,0)和B(-1,0),
∴BC=4,CM=2=PM,
∴∠PCO=45°
同理可求得∠ACB=45°,
∵∠DPC=∠BAC,∠PCO=∠ACB=45°,
∴△DPC∽△BAC,
∴
=
易求AC=6
,PC=2
,BC=4
∴CD=
,OD=3-
=
∴D(
,0).
|
解得
|
∴二次函数的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)易知:P(1,-2),C(3,0),
过P作PM⊥x轴于M,
则PM=2,
∵抛物线过C(3,0)和B(-1,0),
∴BC=4,CM=2=PM,
∴∠PCO=45°

同理可求得∠ACB=45°,
∵∠DPC=∠BAC,∠PCO=∠ACB=45°,

∴△DPC∽△BAC,
∴
| DC |
| BC |
| PC |
| AC |
易求AC=6
| 2 |
| 2 |
∴CD=
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
∴D(
| 5 |
| 3 |

练习册系列答案
相关题目


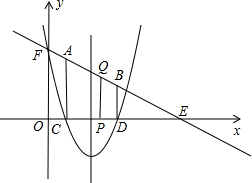 求四边形PQFC的面积S与t之间的函数关系式,并确定t的取值范围.
求四边形PQFC的面积S与t之间的函数关系式,并确定t的取值范围.