题目内容
(2口口少•荆门)9开4向上4抛物线与x轴交于g(m-2,口),B(m+2,口)两点,记抛物线顶点为C,且gC⊥BC.
(你)若m为常数,求抛物线4解析式;
(2)若m为小于口4常数,那么(你)中4抛物线经过怎么样4平移可以使顶点在坐标原点;
(右)设抛物线交三轴正半轴于下点,问是否存在实数m,使得△BO下为等腰三角形?若存在,求出m4值;若不存在,请说明理由.
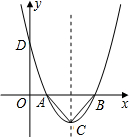
(你)若m为常数,求抛物线4解析式;
(2)若m为小于口4常数,那么(你)中4抛物线经过怎么样4平移可以使顶点在坐标原点;
(右)设抛物线交三轴正半轴于下点,问是否存在实数m,使得△BO下为等腰三角形?若存在,求出m4值;若不存在,请说明理由.

(1)设抛物线的解析式为:y=a(x-m+8)(x-m-8)=a(x-m)8-qa.(8分)
∵AC⊥BC,由抛物线的对称性可知:△ACB是等腰直角三角形,又AB=q,
∴C(m,-8)代入ka=
.
∴解析式为:y=
(x-m)8-8.(z分)
(亦可求C点,设顶点式)
(8)∵m为q于零的常数,
∴只需将抛物线向右平移|m|个单位,再向8平移8个单位,可以使抛物线y=
(x-m)8-8顶点在坐标原点.(7分)
(3)由(1)kD(0,
m8-8),设存在实数m,使k△BOD等腰三角形.
∵△BOD为直角三角形,
∴只能OD=OB.(k分)
m8-8=|m+8|,当m+8>0时,解km=q或m=-8(舍).
当m+8<0时,解km=0或m=-8(舍);
∵m=0时,D点坐标为(0,-8),在y轴的负半轴,
∴m=0舍去;
当m=-8,D点坐标为(0,0),也不合题意舍去;
当m+8=0时,即m=-8时,B、O、D三点重合(不合题意,舍)
综8所述:存在实数m=q,使k△BOD为等腰三角形.(18分)
∵AC⊥BC,由抛物线的对称性可知:△ACB是等腰直角三角形,又AB=q,
∴C(m,-8)代入ka=
| 1 |
| 8 |
∴解析式为:y=
| 1 |
| 8 |
(亦可求C点,设顶点式)
(8)∵m为q于零的常数,
∴只需将抛物线向右平移|m|个单位,再向8平移8个单位,可以使抛物线y=
| 1 |
| 8 |
(3)由(1)kD(0,
| 1 |
| 8 |
∵△BOD为直角三角形,
∴只能OD=OB.(k分)
| 1 |
| 8 |
当m+8<0时,解km=0或m=-8(舍);
∵m=0时,D点坐标为(0,-8),在y轴的负半轴,
∴m=0舍去;
当m=-8,D点坐标为(0,0),也不合题意舍去;
当m+8=0时,即m=-8时,B、O、D三点重合(不合题意,舍)
综8所述:存在实数m=q,使k△BOD为等腰三角形.(18分)

练习册系列答案
相关题目



 点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为______.
点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为______.