题目内容
【题目】阅读理解
在平面直角坐标系
中，两条直线
，
①当
时，
，且
；②当
时，
．
类比应用
（1）已知直线
，若直线
与直线
平行，且经过点
，试求直线
的表达式；
拓展提升
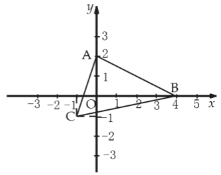
（2）如图，在平面直角坐标系中，
的顶点坐标分别为：
，试求出
边上的高
所在直线的表达式．
【答案】（1）y=2x+5；（2）y=2x+1.
【解析】
(1)利用平行线性质可知k值相等，进而将P点坐标代入
即可求出直线的表达式；
（2）由题意设直线AB的表达式为：y=kx+b，求出直线AB的表达式，再根据题意设AB边上的高CD所在直线的直线表达式为y=mx+n，进行分析求出CD所在直线的表达式.
（1）∵
∥∴
，
∵直线经过点P（-2，1）
∴=2×（-2）+
，=5，
∴直线的表达式为：y=2x+5.
（2）设直线AB的表达式为：y=kx+b
∵直线经过
∴
，解得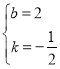
，
∴直线AB的表达式为：
；
设AB边上的高
所在直线的表达式为：y=mx+n，
∵CD⊥AB，
∴
，
∵直线CD经过点C（-1,-1）,
∴
∴
边上的高所在直线的表达式为：y=2x+1.
练习册系列答案
相关题目
【题目】如图，某项研究表明，大拇指与小拇指尽量张开时，两指尖的距离称为指距．如表是测得的指距与身高的一组数据：
指距d（cm） | 19 | 20 | 21 |
身高h（cm） | 151 | 160 | 169 |
（1）你能确定身高h与指距d之间的函数关系式吗？
（2）若某人的身高为196cm，一般情况下他的指距应是多少？
