题目内容
【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2 017次后形成的图形中所有正方形的面积和是( )
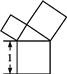

图1 图2
A. 2015 B. 2016 C. 2017 D. 2018
【答案】D
【解析】解:设直角三角形的三条边分别是a,b,c.根据勾股定理,得:a2+b2=c2,即正方形A的面积+正方形B的面积=正方形C的面积=1.推而广之,“生长”了2017次后形成的图形中所有的正方形的面积和是2018×1=2018.故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答问题:
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 30 | 0.15 |
三 | 70.5~80.5 | 50 | 0.25 |
四 | 80.5~90.5 | m | 0.40 |
五 | 90.5~100.5 | n |
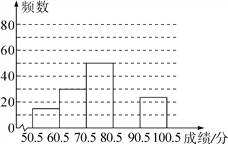
(1)本次抽样调查的样本是__________,样本容量为__________,表中m=__________,n=__________;
(2)补全频数分布直方图;
(3)若抽取的样本具有较好的代表性,且成绩超过80分为优秀,根据样本估计该校八年级学生中汉字听写能力优秀的约有多少人?