题目内容
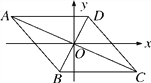
【题目】如图,已知点A(-4,2),B(-1,-2),□ABCD的对角线交于坐标原点O.
(1)请写出点C,D的坐标;
(2)指出从线段AB到线段DC的变换过程;
(3)求□ABCD的面积.
【答案】(1) C(4,-2),D(1,2);(2)把线段AB向右平移5个单位长度可得到线段DC; (3) SABCD=20.
【解析】试题分析:(1)利用中心对称图形的性质得出C,D两点坐标;
(2)利用平行四边形的性质以及结合平移的性质得出即可;
(3)利用![]() 的可以转化为边长为;5和4的矩形面积,进而求出即可.
的可以转化为边长为;5和4的矩形面积,进而求出即可.
试题解析:(1)∵四边形ABCD是平行四边形,
∴四边形ABCD关于O中心对称,
∵A(4,2),B(1,2),
∴C(4,2),D(1,2);
(2)线段AB到线段CD的变换过程是:把线段AB向右平移5个单位长度可得到线段DC.
(3)由(1)得:A到y轴距离为:4,D到y轴距离为:1,
A到x轴距离为:2,B到x轴距离为:2,
∴![]() 的可以转化为边长为;5和4的矩形面积,
的可以转化为边长为;5和4的矩形面积,
∴![]() =5×4=20.
=5×4=20.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】为了增强公民的节水意识,合理利用水资源,某市采用价格调控手段来引导市民节约用水:每户居民每月用水不超过15立方米时,按基本价格x元/立方米进行收费;超过15立方米时,加价收费,超过的部分按y元/立方米收费.该市某户居民今年3、4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
3 | 16 | 50 |
4 | 20 | 70 |
5 | m | 不低于36元且不超过95元 |
(1)求x、y的值;
(2)求该居民5月份用水量m的范围.