题目内容
【题目】如图,点O是边长为4的等边三角形ABC的中心,∠EOF的两边与△ABC的边AB,BC分别交于E、F,∠EOF=120°.
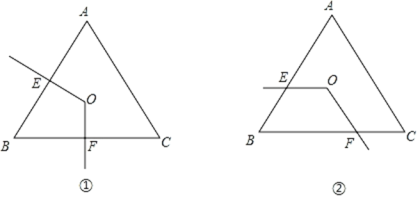
(1)如图①,当E为AB中点时,求∠EOF与△ABC的边所围成的四边形OEBF的面积;
(2)如图②,∠EOF绕点O旋转.在旋转过程中四边形OEBF的面积会改变吗?请说明理由.
【答案】(1)四边形OEBF的面积=![]() ;(2)不变,理由见解析.
;(2)不变,理由见解析.
【解析】
(1)连接OB,由等边三角形的性质可得∠ABO=∠CBO=30°,分别求出OE,OF的长,由面积公式可求解;
(2)连接OB、OC,过点O作ON⊥BC,垂足为N,由“ASA”可证△EOB≌△FOC,可得S△EOB=S△FOC,由面积公式可求解.
解:(1)连接OB,

∵点O是边长为4的等边三角形ABC的中心,
∴∠ABO=∠CBO=30°,
∵当E为AB中点时,
∴AE=BE=2,OE⊥AB,
∴∠BOE=60°,![]() ,
,
∵∠EOF=120°,
∴∠BOF=60°,
∴∠BFO=180°﹣30°﹣60°=90°,
∴BF=CF=2,
∴![]() ,
,
∴四边形OEBF的面积=![]() ;
;
(2)不变,
理由如下:连接OB、OC,过点O作ON⊥BC,垂足为N,
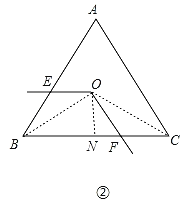
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵点O为△ABC的中心
∴∠OBC=∠OBA=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB.
∠ACB.
∴∠OBA=∠OBC=∠OCB=30°.
∴OB=OC.∠BOC=120°,
∵ON⊥BC,BC=4,
∴BN=NC=2,
∴ON=tan∠OBCBN=![]() ,
,
∴S△OBC=![]() BCON=
BCON=![]() ,
,
∵∠EOF=∠BOC=120°,
∴∠EOF﹣∠BOF=∠BOC﹣∠BOF,即∠EOB=∠FOC,
在△EOB和△FOC中,
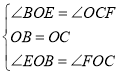
∴△EOB≌△FOC(ASA),
∴S△EOB=S△FOC,
∴![]() =
=![]() .
.