题目内容
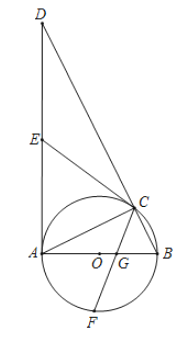
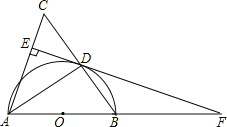
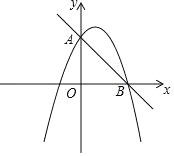
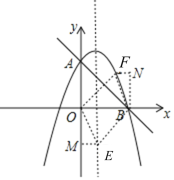
【题目】如图,直线y=﹣x+4与抛物线y=﹣![]() x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
(1)求抛物线的解析式;
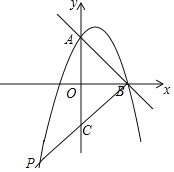
(2)在x轴下方的抛物线上存在一点P,使得∠ABP=90°,求出点P坐标;
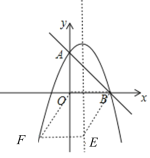
(3)点E是抛物线对称轴上一点,点F是抛物线上一点,是否存在点E和点F使得以点E,F,B,O为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+x+4;(2)P(-4,-8);(3)存在,点F的坐标为(5,
x2+x+4;(2)P(-4,-8);(3)存在,点F的坐标为(5,![]() ),(﹣3,
),(﹣3,![]() ),(3,
),(3,![]() ).
).
【解析】
(1)由直线表达式求出点A、B的坐标,把A、B点坐标代入二次函数表达式,即可求解;
(2)OA=OB=4,则OB为AC的垂直平分线,则点C坐标为(0,-4),求出直线BC的表达式,即可求解;
(3)存在;分OB是平行四边形的一条边或一条对角线两种情况,分别求解即可.
解:(1)在y=﹣x+4中,
当x=0时, y=4,当y=0时,x=4,
即点A、B的坐标分别为(0,4)、(4,0),
将(0,4)、(4,0),代入二次函数表达式,并解得:
b=1,c=4,
抛物线的解析式为:y=﹣![]() x2+x+4;
x2+x+4;
(2)∵OA=OB=4,
∴∠ABO=45°,
∵∠ABP=90°,
则∠PBO=45°,
若直线PB交y轴于点M,
则OM=OB=4,
可得直线BP的解析式为:y=x-4,
联立:y=x-4,y=﹣![]() x2+x+4,得:
x2+x+4,得:
x=4,y=0(即B点);x=-4,y=-8,
即P(-4,-8);
(3)存在;
由y=﹣![]() x2+x+4知抛物线的对称轴为:x=1,
x2+x+4知抛物线的对称轴为:x=1,
设E(1,m),F(n,﹣![]() n2+n+4),O(0,0),B(4,0),
n2+n+4),O(0,0),B(4,0),
①当四边形OBEF是平行四边形时,
有:EF=4,
∴n-1=-4,即n=-3,
F点坐标为(-3,![]() );
);
②当四边形OBFE是平行四边形时,
有:EF=4,
n-1=4,即n=5,
F点坐标为(5,![]() );
);

③当四边形OFBE是平行四边形时,
有: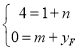 ,
,
即n=3,
F点坐标为(3,![]() );
);
综上所述:点F的坐标为(5,![]() ),(﹣3,
),(﹣3,![]() ),(3,
),(3,![]() ).
).

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案