��Ŀ����
����Ŀ����ͼ1������ABC�У���A=30�㣬��P�ӵ�A������2cm/s���ٶ�������A��C��B�˶�����Q�ӵ�A������a��cm/s�����ٶ���AB�˶���P��Q����ͬʱ��������ijһ���˶�����Bʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊx��s������APQ�����Ϊy��cm2����y����x�ĺ���ͼ����C1��C2������ɣ���ͼ2��ʾ��
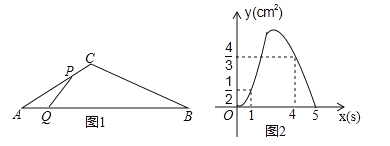
��1����a��ֵ��
��2����ͼ2��ͼ��C2�εĺ�������ʽ��
��3������P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ���������x��ȡֵ��Χ��
���𰸡���1��1����2��![]() ����3��2��x��3��
����3��2��x��3��
��������
�����������1����PD��AB��D������ֱ�������ε����ʵõ�PD=![]() AP=x�����������ε������ʽ�õ���������ʽ��������㣻
AP=x�����������ε������ʽ�õ���������ʽ��������㣻
��2�����ݵ�x=4ʱ��y=![]() �����sinB���õ�ͼ��C2�εĺ�������ʽ��
�����sinB���õ�ͼ��C2�εĺ�������ʽ��
��3�����![]() �����ֵ�����ݶ��κ��������ʼ��㼴�ɣ�
�����ֵ�����ݶ��κ��������ʼ��㼴�ɣ�
�����������1����ͼ1����PD��AB��D���ߡ�A=30�㣬��PD=![]() AP=x����y=
AP=x����y=![]() AQPD=
AQPD=![]() ����ͼ���֪����x=1ʱ��y=
����ͼ���֪����x=1ʱ��y=![]() ����
����![]() ��a��12=
��a��12=![]() ����ã�a=1��
����ã�a=1��
��2����ͼ2����PD��AB��D����ͼ���֪��PB=5��2��2x=10��2x��PD=PBsinB=��10��2x��sinB����y=![]() ��AQ��PD=
��AQ��PD=![]() x����10��2x��sinB������x=4ʱ��y=
x����10��2x��sinB������x=4ʱ��y=![]() ����
����![]() ��4����10��2��4��sinB=
��4����10��2��4��sinB=![]() ����ã�sinB=
����ã�sinB=![]() ����y=
����y=![]() x����10��2x����
x����10��2x����![]() ����
����![]() ��
��
��3��![]() ����ã�x1=0��x2=2����ͼ���֪����x=2ʱ��
����ã�x1=0��x2=2����ͼ���֪����x=2ʱ��![]() �����ֵ�����ֵ��
�����ֵ�����ֵ��![]() ��22=2��
��22=2��![]() =2����ã�x1=3��x2=2������2��x��3ʱ����P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ�������
=2����ã�x1=3��x2=2������2��x��3ʱ����P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ�������


����Ŀ���������б��еĶ�Ӧֵ��
x | 2.1 | 2.2 | 2.3 | 2.4 |
ax2+bx+c | ��1.39 | ��0.76 | ��0.11 | 0.56 |
�жϷ���ax2+bx+c=0��a��0��a��b��cΪ��������һ�����ȡֵ��ΧΪ ��