题目内容
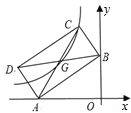
【题目】如图,将直角三角板![]() 的直角边
的直角边![]() 放在半圆
放在半圆![]() 的直径
的直径![]() 上,直角顶点
上,直角顶点![]() 与直径端点
与直径端点![]() 重合,已知
重合,已知![]() ,且
,且![]() 的直角边
的直角边![]() 与半圆
与半圆![]() 的半径
的半径![]() 长均为2.现将直角三角板
长均为2.现将直角三角板![]() 沿直径
沿直径![]() 的方向向右平移,将三角板
的方向向右平移,将三角板![]() 平移后的三角形记为
平移后的三角形记为![]() .
.
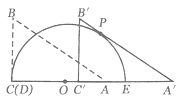
(1)如图,当![]() 平移到斜边与半圆相切时,试求
平移到斜边与半圆相切时,试求![]() 的长度(结果保留
的长度(结果保留![]() );
);
(2)设平移距离为![]() ,在直角三角形
,在直角三角形![]() 平移过程中,折线
平移过程中,折线![]() (包括端点)与半圆弧共有3个交点时,求
(包括端点)与半圆弧共有3个交点时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 且
且![]()
【解析】
(1)先根据圆的切线的性质得出![]() ,再根据三角形的外角性质得出
,再根据三角形的外角性质得出![]() ,然后根据弧长公式即可得;
,然后根据弧长公式即可得;
(2)先找出三个临界位置:![]() 与
与![]() 重合时、
重合时、![]() 与
与![]() 重合时、
重合时、![]() 与半圆相切时,再分别解直角三角形即可得.
与半圆相切时,再分别解直角三角形即可得.
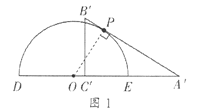
(1)如图1,![]() 切半圆
切半圆![]() 于点
于点![]() ,连接
,连接![]()
则![]()
![]()
在![]() 中,
中,![]()
![]()
![]() 的长度为
的长度为![]() ;
;
(2)由平移的性质可得:![]()
![]()
由题意,可分以下三个临界位置:
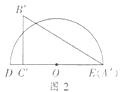
①如图2,![]() 与
与![]() 重合时
重合时
在![]() 中,
中,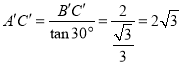
![]()
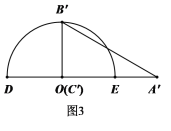
②如图3,![]() 与
与![]() 重合时
重合时
![]()
③由(1)知,![]() 与半圆相切时(如图1)
与半圆相切时(如图1)
在![]() 中,
中,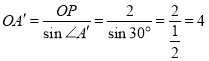
又![]()
![]()
![]()
综上,![]() 且
且![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校为了解八年级学生睡眠时间的情况,随机调查了该校八年级 50 名学生,得到了一天睡眠时间的一组样本数据,如下:
睡眠时间 | 组中值 | 频数 |
|
| 3 |
| 6 | 3 |
| 7 |
|
| 8 | 25 |
| 9 | 10 |
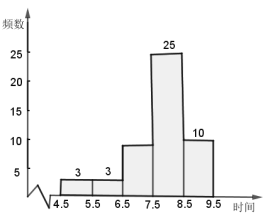
根据以上统计图表完成下列问题:
(1)统计表中![]() ;
;![]() ;
;
(2)根据数据,估算该校八年级学生平均每天睡眠时间;
(3)睡眠时间为 4.5~5.5h 的 3 名同学中有 1 名男生和 2 名女生,现从中随机挑选 2 名同学去医院进行健康体检,请用树状图法或列表法求出恰好选中“1 男 1 女”的概率.