Question

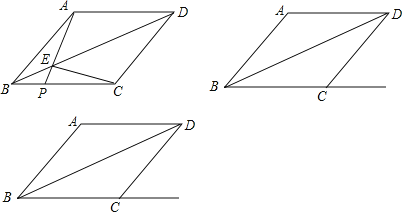
【题目】如图，菱形ABCD中，AB＝10，连接BD，点P是射线BC上一点（不与点B重合），AP与对角线BD交于点E，连接EC．

（1）求证：AE＝CE；

（2）若sin∠ABD＝，当点P在线段BC上时，若BP＝4，求△PEC的面积；

（3）若∠ABC＝45°，当点P在线段BC的延长线上时，请直接写出△PEC是等腰三角形时BP的长．

Answer 1

【答案】（1）详见解析；（2）；（3）△PEC是等腰三角形时BP的长为10或．

【解析】

(1)由菱形的性质得出∠ABE=∠CBE，AB=BC，由SAS证得△ABE≌△CBE，即可得出结论；
(2)连接AC，交BD于O，证明△BEP∽△DEA，，则，求出OA=2，，BD=8，，，S△DEA，S△ABE=S△BEC，S△BEP=，即可得出答案；

(3) ①当CE=CP时，得出△PEC是等腰直角三角形，过点E作EF∥AB交BC于F，证出EF=BF，推出CF+CF=BC=10，求出CF的长，即可得出答案；
②当CE=CP时，求得∠CPE=30°，∠BAE=∠BCE=105°，过点A作AN⊥BP于N，则△ABN是等腰直角三角形，得出AN=BN=AB=5，求出PN=5，即可得出答案．

(1)∵四边形ABCD是菱形，

∴∠ABE=∠CBE，AB=BC，

在△ABE和△CBE中，，

∴△ABE≌△CBE(SAS)，

∴AE=CE；

(2)连接AC，交BD于O，如图1所示：

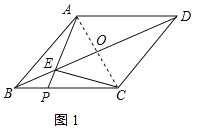
∵四边形ABCD是菱形，

∴AD∥BC，AD=AB=10，∠AOB=90°，OB=OD，OA=OC，

∴△BEP∽△DEA，

∴，

∴，

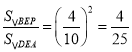∵sin∠ABD=，

∴OA=2，

，

∴BD=2OB=8，

∵，

∴，

解得：，

∴，

∴S△DEA=OADE=×2×，

S△ABE=OABE=×2×S△BEC，

∴S△BEP=S△DEA=×=，

∴S△PEC=S△BEC﹣S△BEP==；

(3)①当CE=CP时，

∴∠CPE=∠CEP，

由(1)得：△ABE≌△CBE，

∴∠BAE=∠BCE，

∴∠BAE=∠BCE=∠CPE+∠CEP=2∠CPE，

∵∠ABC+∠BAE+∠CPE=180°，∠ABC=45°，

∴45°+2∠CPE+∠CPE=180°，

解得：∠CPE=45°，∠BAE=∠BCE=90°，

∴∠ECP=90°，

∴△PEC是等腰直角三角形，

过点E作EF∥AB交BC于F，如图所示：

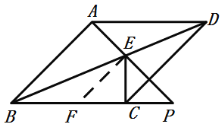
∴∠EFP=∠ABC=45°，∠FEP=∠BAP=90°，∠BEF=∠ABE=∠EBC，

∴∠FEC=∠FEP-∠CEP=90°-45°=45°，EF=BF，

则CE=CP=CF，EF=CF，

∴CF+CF=BC=10，

∴CF=，

∴BP=BC+CP=BC+CF=10+=10；

②当CE=CP时，

∴∠PCE=∠CEP，

由(1)得：△ABE≌△CBE，

∴∠AEB=∠CEB，

∴∠BAE=∠BCE=∠CPE+∠CEP=∠CPE+，

∵∠ABC+∠BAE+∠CPE=180°，∠ABC=45°，

∴45°+∠CPE++∠CPE=180°，

解得：∠CPE=30°，∠BAE=∠BCE=105°，

过点A作AN⊥BP于N，如图3所示：

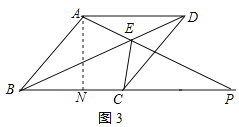
∵∠ABC=45°，

则△ABN是等腰直角三角形，

∴AN=BN=AB=5，

∵∠APB=30°，

∴tan30°=，即，

∴PN=5，

∴BP=BN+PN=5+5，

综上所述，△PEC是等腰三角形时BP的长为10或．