题目内容
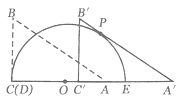
【题目】如图,△ABC是等边三角形,点D为BC边上一点,DC=2BD=4,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕D点旋转一周,当AE取最小值时,AG的长为____

【答案】8
【解析】
点A作AM⊥BC于M,由已知得出BD=2,得出BC=BD+DC=6,由等边三角形的性质得出AB=AC=BC=6,BM=3,得出DM=BMBD=1,在Rt△ABM中,由勾股定理得出AM=![]() ,当正方形DEFG绕点D旋转到点E、A、D在同一条直线上时,AD+AE=DE,即此时AE取最小值,在Rt△ADM中,由勾股定理得出AD=
,当正方形DEFG绕点D旋转到点E、A、D在同一条直线上时,AD+AE=DE,即此时AE取最小值,在Rt△ADM中,由勾股定理得出AD=![]() ,在Rt△ADG中,由勾股定理即可得出AG=8
,在Rt△ADG中,由勾股定理即可得出AG=8
解:过点A作AM⊥BC于M,
∵DC=2BD=4,
∴BD=2,
∴BC=BD+DC=2+4=6,
∵△ABC是等边三角形,
∴AB=AC=BC=6,
∵AM⊥BC,
∴BM=![]() BC=3,
BC=3,
∴DM=BMBD=32=1,
在Rt△ABM中,AM=![]() ,
,
如图,当点E在DA延长线上时,AE=DEAD.
此时AE取最小值,
在Rt△ADM中,AD=![]() ,
,
∵四边形形DEFG是正方形,
∴∠ADG=90°,GD=DE=BC=6,
∴在Rt△ADG中,AG=![]() ,
,
故答案为:8.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】每年4月23日是世界读书日,某校为了解学生课外阅读情况,随机抽取20名学生,对每人每周用于课外阅读的平均时间(单位:min)进行调查,过程如下:
收集数据:
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:
课外阅读平均时间x(min) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等级 | D | C | B | A |
人数 | 3 | a | 8 | b |
分析数据:
平均数 | 中位数 | 众数 |
80 | m | n |
请根据以上提供的信息,解答下列问题:
(1)填空:a= ,b= ;m= ,n= ;
(2)已知该校学生500人,若每人每周用于课外阅读的平均时间不少于80min为达标,请估计达标的学生数;
(3)设阅读一本课外书的平均时间为260min,请选择适当的统计量,估计该校学生每人一年(按52周计)平均阅读多少本课外书?