��Ŀ����
����Ŀ��ijˮ���̵���12.5Ԫ/ǧ�˵ļ۸�һ��ˮ���������ۣ�����������������5%�����������0.8Ԫ/ǧ�ˣ�������ð��ս����������㣩�����費���������ã�
��1���̵�Ҫ��ˮ��������������Ϊ����Ԫ�Ų��������
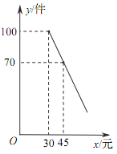
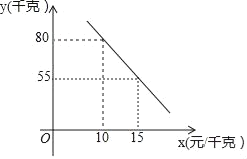
��2�������۹����У��̵귢��ÿ��ˮ����������y��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�֮��ĺ�����ϵ��ͼ��ʾ����ô�����۵��۶�Ϊ����ʱ��ÿ���õ�����w�����������Ƕ��٣�
��3�����̵����ÿ����1ǧ��ˮ���;���pԪ����p��1����ϣ�����̣�ͨ�����ۼ�¼���֣����ۼ۸����ÿǧ��22Ԫʱ���۳�������ÿ���������x�������С��ֱ��д��p��ȡֵ��Χ��
���𰸡���1��ˮ����Ҫ��ˮ���ۼ����ٶ�Ϊ14Ԫ/ǧ�˲Ų��������2�������۵��۶�Ϊ20Ԫʱ��ÿ���õ�����w������������180Ԫ��3��1��p��4
��������
��1���蹺��ˮ��aǧ�ˣ�ˮ���ۼ۶�ΪmԪ/ǧ�ˣ�ˮ���̲Ų�����������������г�����ʽ������⣻
��2���ɣ�1����y�����۵���x֮��ĺ�����ϵΪ��y����5x+130������w����x��14��y�õ����κ������ɽ�����⣻
��3����۳�����������Ϊs����s����x��14��p������5x+130�������ݶԳ����뺯�������ʼ������.
��1���蹺��ˮ��aǧ�ˣ�ˮ���ۼ۶�ΪmԪ/ǧ�ˣ�ˮ���̲Ų������������
am��1��5%���ݣ�12.5+0.8��a
��a��0�ɽ�ã�m��14
��ˮ����Ҫ��ˮ���ۼ����ٶ�Ϊ14Ԫ/ǧ�˲Ų������
��2���ɣ�1����֪��ÿǧ��ˮ����ƽ���ɱ�Ϊ14Ԫ
��y�����۵���x֮��ĺ�����ϵΪ��y����5x+130
������ã�w����x��14��y����x��14������5x+130������5x2+200x��1820
������w����5��x��20��2+180
�൱x��20ʱ��w�����ֵ
�൱���۵��۶�Ϊ20Ԫʱ��ÿ���õ�����w������������180Ԫ��
��3����۳�����������Ϊs
��s����x��14��p������5x+130������5x2+��5p+200��x��130��p+14��
�������ߵĿ�������
��Գ���Ϊֱ��x��![]() ��
��![]()
�����ۼ۸����ÿǧ��22Ԫʱ���۳�������ÿ�������s��x���������С
��![]() ��22
��22
���p��4
��1��p��4

 ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д�