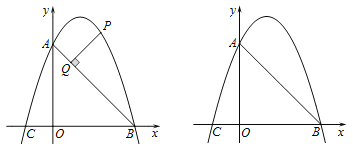题目内容
【题目】如图抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线对称轴上任意一点,若点
是抛物线对称轴上任意一点,若点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则
,则![]() 的最小值为_____.
的最小值为_____.
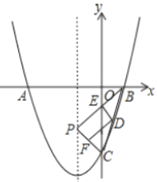
【答案】![]()
【解析】
连接![]() ,交对称轴于点
,交对称轴于点![]() ,先通过解方程
,先通过解方程![]() ,得
,得![]() ,
,![]() ,通过
,通过![]() ,得
,得![]() ,于是利用勾股定理可得到
,于是利用勾股定理可得到![]() 的长;再根据三角形中位线性质得
的长;再根据三角形中位线性质得![]() ,
,![]() ,所以
,所以![]() ;由点
;由点![]() 在抛物线对称轴上,
在抛物线对称轴上,![]() 、
、![]() 两点为抛物线
两点为抛物线![]() 与
与![]() 轴的交点,得
轴的交点,得![]() ;利用两点之间线段最短得到此时
;利用两点之间线段最短得到此时![]() 的值最小,其最小值为
的值最小,其最小值为![]() 的长,从而得到
的长,从而得到![]() 的最小值.
的最小值.
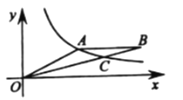
如图,连接![]() ,交对称轴于点
,交对称轴于点![]() ,则此时
,则此时![]() 最小.
最小.

∵ 抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,
∴当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵ 点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,
的中点,
∴ ![]() ,
,![]() ,
,
∴![]() ,
,
∵点![]() 在抛物线对称轴上,
在抛物线对称轴上,![]() 、
、![]() 两点为抛物线
两点为抛物线![]() 与
与![]() 轴的交点,
轴的交点,
∴![]() ,
,
∴![]() ,
,
∴此时![]() 的值最小,其最小值为
的值最小,其最小值为![]() ,
,
∴![]() 的最小值为:
的最小值为:![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目