题目内容
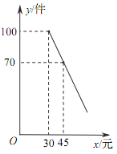
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
【答案】(1)![]() ;(2)
;(2)![]() 时,w最大
时,w最大![]() ;(3)
;(3)![]() 时,每天的销售量为20件.
时,每天的销售量为20件.
【解析】
(1)将点(30,150)、(80,100)代入一次函数表达式,即可求解;
(2)由题意得w=(x-30)(-2x+160)=-2(x-55)2+1250,即可求解;
(3)由题意得(x-30)(-2x+160)≥800,解不等式即可得到结论.
(1)设y与销售单价x之间的函数关系式为:y=kx+b,
将点(30,100)、(45,70)代入一次函数表达式得:
![]() ,
,
解得:![]() ,
,
故函数的表达式为:y=-2x+160;
(2)由题意得:w=(x-30)(-2x+160)=-2(x-55)2+1250,
∵-2<0,故当x<55时,w随x的增大而增大,而30≤x≤50,
∴当x=50时,w由最大值,此时,w=1200,
故销售单价定为50元时,该超市每天的利润最大,最大利润1200元;
(3)由题意得:(x-30)(-2x+160)≥800,
解得:x≤70,
∴每天的销售量y=-2x+160≥20,
∴每天的销售量最少应为20件.

练习册系列答案
相关题目