题目内容
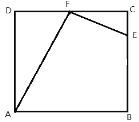
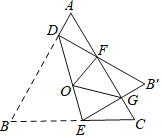
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
【答案】D
【解析】A、根据等边三角形ABC的外心的性质可知:AO平分∠BAC,根据角平分线的定理和逆定理得:FO平分∠DFG,由外角的性质可证明∠DOF=60°,同理可得∠EOG=60°,∠FOG=60°=∠DOF=∠EOG,可证明△DOF≌△GOF≌△GOE,△OAD≌△OCG,△OAF≌△OCE,可得AD=CG,AF=CE,从而得△ADF≌△CGE;
B、根据△DOF≌△GOF≌△GOE,得DF=GF=GE,所以△ADF≌△B'GF≌△CGE,可得结论;
C、根据S四边形FOEC=S△OCF+S△OCE,依次换成面积相等的三角形,可得结论为:S△AOC=![]() S△ABC(定值),可作判断;
S△ABC(定值),可作判断;
D、方法同C,将S四边形OGB'F=S△OAC-S△OFG,根据S△OFG=![]() FGOH,FG变化,故△OFG的面积变化,从而四边形OGB'F的面积也变化,可作判断.
FGOH,FG变化,故△OFG的面积变化,从而四边形OGB'F的面积也变化,可作判断.
A、连接OA、OC,
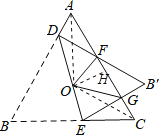
∵点O是等边三角形ABC的外心,
∴AO平分∠BAC,
∴点O到AB、AC的距离相等,
由折叠得:DO平分∠BDB',
∴点O到AB、DB'的距离相等,
∴点O到DB'、AC的距离相等,
∴FO平分∠DFG,
∠DFO=∠OFG=![]() (∠FAD+∠ADF),
(∠FAD+∠ADF),
由折叠得:∠BDE=∠ODF=![]() (∠DAF+∠AFD),
(∠DAF+∠AFD),
∴∠OFD+∠ODF=![]() (∠FAD+∠ADF+∠DAF+∠AFD)=120°,
(∠FAD+∠ADF+∠DAF+∠AFD)=120°,
∴∠DOF=60°,
同理可得∠EOG=60°,
∴∠FOG=60°=∠DOF=∠EOG,
∴△DOF≌△GOF≌△GOE,
∴OD=OG,OE=OF,
∠OGF=∠ODF=∠ODB,∠OFG=∠OEG=∠OEB,
∴△OAD≌△OCG,△OAF≌△OCE,
∴AD=CG,AF=CE,
∴△ADF≌△CGE,
故选项A正确;
B、∵△DOF≌△GOF≌△GOE,
∴DF=GF=GE,
∴△ADF≌△B'GF≌△CGE,
∴B'G=AD,
∴△B'FG的周长=FG+B'F+B'G=FG+AF+CG=AC(定值),
故选项B正确;
C、S四边形FOEC=S△OCF+S△OCE=S△OCF+S△OAF=S△AOC=![]() S△ABC(定值),
S△ABC(定值),
故选项C正确;
D、S四边形OGB'F=S△OFG+S△B'GF=S△OFD+△ADF=S四边形OFAD=S△OAD+S△OAF=S△OCG+S△OAF=S△OAC-S△OFG,
过O作OH⊥AC于H,
∴S△OFG=![]() FGOH,
FGOH,
由于OH是定值,FG变化,故△OFG的面积变化,从而四边形OGB'F的面积也变化,
故选项D不一定正确;
故选:D.