题目内容
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用![]() 万元
万元![]() 与年产量
与年产量![]() 万件
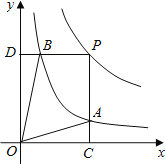
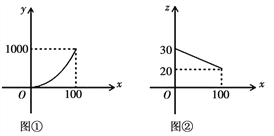
万件![]() 之间的函数图象是顶点为原点的抛物线的一部分
之间的函数图象是顶点为原点的抛物线的一部分![]() 如图
如图![]() 所示
所示![]() ;该产品的销售单价
;该产品的销售单价![]() 元
元![]() 件
件![]() 与年销售量
与年销售量![]() 万件
万件![]() 之间的函数图象是如图
之间的函数图象是如图![]() 所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元
所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元![]() 毛利润
毛利润![]() 销售额
销售额![]() 生产费用
生产费用![]()
![]() 请写出y与x以及z与x之间的函数关系式;
请写出y与x以及z与x之间的函数关系式;
![]() 求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
【答案】(1) ![]() ,
,![]() ;(2) 当
;(2) 当![]() 时,W有最大值1125,
时,W有最大值1125,![]() 年产量为75
年产量为75
万件时毛利润最大,最大毛利润为1125万元;
【解析】分析:(1)利用待定系数法可求出y与x以及z与x之间的函数关系式;
(2)根据(1)的表达式及毛利润=销售额-生产费用,可得出w与x之间的函数关系式,再利用配方法求函数最值即可;
详解:![]() 图
图![]() 可得函数经过点
可得函数经过点![]() ,
,
设抛物线的解析式为![]() ,
,
将点![]() 代入得:
代入得:![]() ,
,
解得:![]() ,
,
故y与x之间的关系式为![]() .
.
图![]() 可得:函数经过点
可得:函数经过点![]() 、
、![]() ,
,
设![]() ,则
,则![]() ,
,
解得: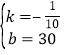 ,
,
故z与x之间的关系式为![]() ;
;
(2)![]()
![]()
∵![]()
∴当x=75时,W有最大值1125,
∴年产量为75万件时毛利润最大,最大毛利润为1125万元;

【题目】(1)在下列表格中填上相应的值
x | … | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | … |
| … | -1 | -2 | 3 | 1 | … |

(2)若将上表中的变量![]() 用y来代替(即有
用y来代替(即有![]() ),请以表中的
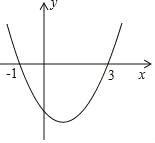
),请以表中的![]() 的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
(3)在(2)的条件下,可将y看作是x的函数 ,请你结合你所画的图像,写出该函数图像的两个性质 :__________________________________________________.
(4)结合图像,借助之前所学的函数知识,直接写出不等式![]() 的解集: ____________
的解集: ____________