题目内容
【题目】（1）在下列表格中填上相应的值
x | … | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | … |
| … | -1 | -2 | 3 | 1 | … |
（2）若将上表中的变量
用y来代替（即有
），请以表中的
的值为点的坐标， 在下方的平面直角坐标系描出相应的点，并用平滑曲线顺次连接各点
（3）在（2）的条件下，可将y看作是x的函数 ，请你结合你所画的图像，写出该函数图像的两个性质 ：__________________________________________________.
（4）结合图像，借助之前所学的函数知识，直接写出不等式
的解集： ____________
【答案】 该函数图形是一个轴对称（中心对称）（即是轴对称又是中心对称）图形 
或
【解析】分析：（1）计算后完成表格即可；
（2）作出函数图象即可；
（3）根据图象得出函数的性质即可；
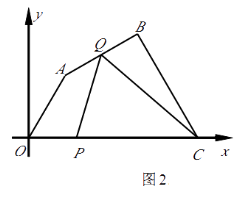
（4）再同一坐标系中，作出
和y=x+1的图象，求出交点A，B的坐标，根据图象得出结论，
详解：（1）填表如下：
x | … | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | … |
| … | -1 | - | -2 | -3 | -6 | 6 | 3 | 2 |
| 1 | … |
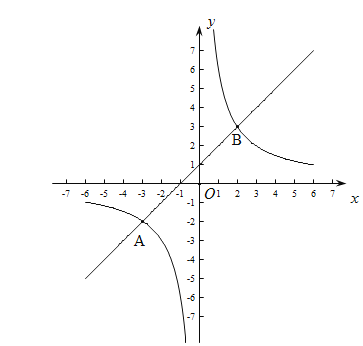
（2）如图：
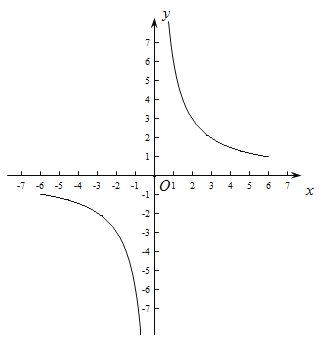
（3） 本题答案是开放式的，学生答出某两个性质即可：
如从函数图像对称性来说：该函数图形是一个轴对称（中心对称）（即是轴对称又是中心对称）图形或该函数经过一、三象限或该函数在每个象限内，y随x增大而增小（x＞0 或x＜0， y随x增大而增小）等或与x轴y轴无交点；
（4）再同一坐标系中，作出和y=x+1的图象，如图所示， 解得：A（-3，-2），B（2，3）， 由图象可知：不等式
的解集为：
或
．
练习册系列答案
相关题目
