题目内容
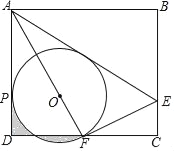
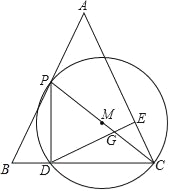
【题目】在△ABC中,AB=AC=2![]() ,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
【答案】![]()
【解析】
作AH⊥BC于H.首先证明△PDB∽△DEC∽△CEG∽△AHB,设BD=a,则有PD=PG=2a,CD=4-a,EC=![]() ,CG=
,CG=![]() ,推出PC=PG+CG=
,推出PC=PG+CG=![]() ,在Rt△PCD中,根据PD2+CD2=PC2,构建方程即可解决问题.
,在Rt△PCD中,根据PD2+CD2=PC2,构建方程即可解决问题.
如图,作AH⊥BC于H,
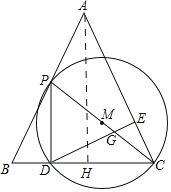
∵AB=AC=2![]() ,AH⊥BC,
,AH⊥BC,
∴∠B=∠ACD,BH=CH=2,AH=![]() =4,
=4,
∵PC是直径,
∴∠PDC=90°,
∵DE⊥AC,
∴∠CDP=∠CED=90°,
∵PD=PG,
∴∠PDG=∠PGD=∠CGE,
∵∠PDG+∠CDE=90°,∠CDE+∠ECD=90°,
∴∠PDG=∠ECD=∠B=∠EGC,
∵∠PDB=∠DEC=∠AHB=90°,
∴△PDB∽△DEC∽△CEG∽△AHB,设BD=a,
则有PD=PG=2a,CD=4-a,EC=![]() ,CG=
,CG=![]() ,
,
∴PC=PG+CG=![]() ,
,
在Rt△PCD中,∵PD2+CD2=PC2,
∴4a2+(4-a)2=(![]() )2,
)2,
解得a=![]() 或4(舍弃),
或4(舍弃),
∴BD=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目