题目内容
【题目】已知二次函数y1=x2+2x+m﹣5.
(1)如果该二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如果该二次函数的图象与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(1,0),求它的表达式和点C的坐标;
(3)如果一次函数y2=px+q的图象经过点A、C,请根据图象直接写出y2<y1时,x的取值范围.
【答案】
(1)解:∵二次函数y1=x2+2x+m﹣5的图象与x轴有两个交点,
∴△>0,
∴22﹣4(m﹣5)>0,
解得:m<6
(2)解:∵二次函数y1=x2+2x+m﹣5的图象经过点(1,0),
∴1+2+m﹣5=0,
解得:m=2,
∴它的表达式是y1=x2+2x﹣3,
∵当x=0时,y=﹣3,
∴C(0,﹣3)
(3)解:由图象可知:当y2<y1时,x的取值范围是x<﹣3或x>0.
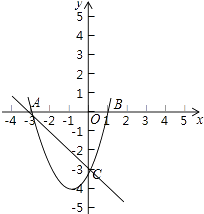
【解析】(1)根据该二次函数的图象与x轴有两个交点可知判别式>0,进而可求出m的范围;
(2)根据该二次函数的图象过点B(1,0),从而求出m的值,可得它的表达式,再由x=0,求得y的值,则可得C的坐标;
(3)根据题意画出图象,再由图象可直接求得.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目