题目内容
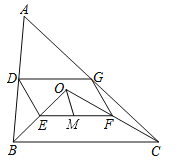
【题目】已知如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3: 5,AE=8,BD=4,求DC的长.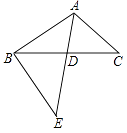
【答案】解:∵∠C=∠E,∠ADC=∠BDE,
∴△ADC∽△BDE,
∴ ![]() ,
,
又∵AD:DE=3:5,AE=8,
∴AD=3,DE=5,
∵BD=4,
∴ ![]() ,即
,即 ![]() .
.
∴DC= ![]() .
.
【解析】由AD:DE=3:5,AE=8,可求出AD、DE的长,利用两对应角相等来证明△ADC∽△BDE,根据相似三角形的对应边成比例可求出DC的长.
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方).

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目