题目内容
【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
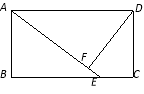
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
【答案】(1)相似、理由见解析;(2)7.2
【解析】
试题分析:(1)根据DF⊥AE和矩形得出∠AFD=∠B,根据AD∥BC得出∠DAE=∠AEB,从而得出三角形相似;(2)根据Rt△ABE的勾股定理得出AE的长度,然后根据三角形相似得出DF的长度.
试题解析:(1)∵DF⊥AE ∴∠AFD=90° ∵矩形ABCD,∴∠B=90°=∠AFD
∵AD∥BC ∴∠DAE=∠AEB ∴△ABE∽△DFA;
(2)∵AB=6,BE=8,∠B=90° ∴AE=10 ∵△ABE∽△DFA
∴![]() =
=![]() 即
即![]() =
=![]() ∴DF=7.2.
∴DF=7.2.

练习册系列答案
相关题目
【题目】某商店积压了100件某种商品,为使这批货物尽快脱手,该商店采取了如下销售方案,将价格提高到原来的2.5倍,再作3次降价处理;第一次降价30%,标出“亏本价”;第二次降价30%,标出“破产价”;第三次降价30%,标出“跳楼价”.3次降价处理销售结果如下表:
降价次数 | 一 | 二 | 三 |
销售件数 | 10 | 40 | 一抢而光 |
(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪种方案更盈利?