��Ŀ����
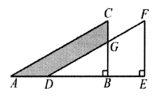
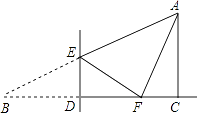
����Ŀ����֪����ͼ������ABC�У���C��90������B��30����AC��6��ADƽ�֡�CAB��BC��D��EΪ����AC�ϵ�һ�����㣬EF��AD������AB�ڵ�F������DF��
��1����DB�ij���
��2������E���߶�AC��ʱ����AE��x��S��BDF��y����y����x�ĺ�������ʽ����S��BDF��ʾ��BDF�������
��3����AEΪ��ֵʱ����BDF�ǵ��������Σ�����ֱ��д���𰸣�����д�����̣�
���𰸡���1��BC��4![]() ����2��y����
����2��y����![]() x+12
x+12![]() ��0��x��6������3����AE��ֵΪ0��12��4
��0��x��6������3����AE��ֵΪ0��12��4![]() ��12+4
��12+4![]() ʱ����BDF�ǵ��������Σ�
ʱ����BDF�ǵ��������Σ�
��������
��1�����ݺ�30�Ƚǵ�ֱ�������οɵ�AB��BC�ij�����ADƽ�֡�CAB�ɵá�CAD��![]() ��CAB��30������ֱ�������οɵ�CD�ij�����DB��BC��CD��
��CAB��30������ֱ�������οɵ�CD�ij�����DB��BC��CD��
��2����ͼ1�У���DH��AB��H�����ݽ�ƽ���ߵ����ʿɵ�DC��DH��2![]() ���ٸ�����֪ADƽ�֡�CAB��EF��AD֤����AEG����AFG����AE��AF��x��BF��12��x���������ε�������㹫ʽ���ɵ�y����x�ĺ�������ʽ��ע��x��ȡֵ��Χ��
���ٸ�����֪ADƽ�֡�CAB��EF��AD֤����AEG����AFG����AE��AF��x��BF��12��x���������ε�������㹫ʽ���ɵ�y����x�ĺ�������ʽ��ע��x��ȡֵ��Χ��
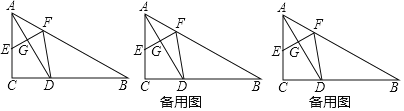
��3��������������ٵ���E��A�غ�ʱ����BDF�ǵ��������Σ��ڵ���E���߶�AC�ϣ�BD��BFʱ����BDF�ǵ��������Σ��۵���E���߶�AC���ӳ����ϣ�BF��BDʱ����BDF�ǵ��������Σ��ֱ����AE��ֵ����.
��1����Rt��ABC�У��ߡ�C��90������B��30����AC��6��
���CAB��60����AB��2AC��12��BC��![]() AC��6
AC��6![]() ��
��
��ADƽ�֡�CAB��BC��D��
���CAD��![]() ��CAB��30����
��CAB��30����
��CD��ACtan30����2![]() ��
��
��DB��BC��CD��6![]() ��2
��2![]() ��4
��4![]() ��
��
��2����ͼ1�У���DH��AB��H��
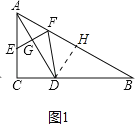
��DAƽ�֡�CAB��DC��AC��DH��AB��
��DC��DH��2![]() ��
��
��EF��AD��
���AGE����AGF��90����
�ߡ�EAG����FAG����AEG+��EAG��90������AFG+��FAG��90����
���AEG����AFG��
��AE��AF��x��
��BF��12��x��
��S��BDF��![]() BFDH��
BFDH��![]() ��12��x��2
��12��x��2![]() ����
����![]() x+12
x+12![]() ��0��x��6����
��0��x��6����
��y=��![]() x+12
x+12![]() ��0��x��6����
��0��x��6����
��3���ٵ���E��A�غ�ʱ����BDF�ǵ��������Σ���ʱx��0����AE��0��
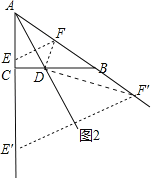
����ͼ2�У���BD��BFʱ��
��BD��4![]() ��
��
��BF��4![]() ��
��
��AE��AF��AB��BF��12��4![]() ��
��
����ͼ2�У���BF��BD=4![]() ʱ��
ʱ��
��AE��AF����AB+BF����12+4![]() ��
��
������������AE��ֵΪ0��12��4![]() ��12+4
��12+4![]() ʱ����BDF�ǵ��������Σ�
ʱ����BDF�ǵ��������Σ�
�ʴ�Ϊ����1��BC��4![]() ����2��y����
����2��y����![]() x+12
x+12![]() ��0��x��6������3����AE��ֵΪ0��12��4
��0��x��6������3����AE��ֵΪ0��12��4![]() ��12+4
��12+4![]() ʱ����BDF�ǵ��������Σ�
ʱ����BDF�ǵ��������Σ�