题目内容
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.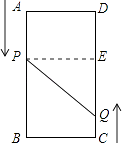
(1)问几秒后,点P和点Q的距离是10cm?
(2)问几秒后,以P、Q、D三点为顶点的三角形为直角三角形?
(提示:根据不同情况画出不同的图形,再给予解决问题.)
【答案】
(1)解:设x秒后,点P和点Q的距离是10cm,
(16﹣2x﹣3x)2+62=102,
(16﹣5x)2=64,
16﹣5x=±8,
x1=1.6,x2=4.8,
答:1.6秒或4.8秒时,点P和点Q的距离是10cm;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=16,AD=BC=6,
根据题意得:AP=3t,CQ=2t,
∴DQ=CD﹣CQ=16﹣2t,
过点Q作QM⊥AB于点M,
∴四边形BCQM是矩形,
∴QM=BC=6,BM=CQ=2t,
∴PM=AB﹣AP﹣BM=16﹣5t,
①如图1, 
若∠DPQ=90°,
∴∠APD+∠MPQ=90°,
∵∠APD=∠ADP=90°,
∴∠ADP=∠MPQ,
∵∠A=∠PMQ=90°,
∴△APD∽△MQP,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:t=2或t= ![]() ;
;
②如图2, 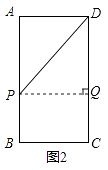
若∠DQP=90°,则有DQ2=DP2﹣PQ2,
∴(16﹣2t)2=62+(3t)2﹣62,
解得:t= ![]() ,
,
综上所述,当t=2或 ![]() 或
或 ![]() 时,△PDQ为直角三角形.
时,△PDQ为直角三角形.
【解析】(1)根据矩形的性质和勾股定理,得到一元二次方程,求出这个一元二次方程的解即可;(2)根据矩形的性质和速度得到各个边的关系式,当∠DPQ=90°时,得到△APD∽△MQP,得到比例求出t的值;当∠DQP=90°时,根据勾股定理求出t的值,在解一元二次方程时,注意实际意义.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案