题目内容
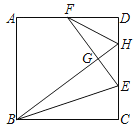
【题目】如图，在ABCD中，以点A为圆心AB长为半径画弧交AD于点F，再分别以点B，F为圆心，大于
BF的长度为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF．
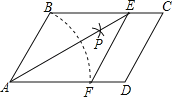
（1）求证：四边形ABEF是菱形；
（2）若∠C＝60°，AE＝4
，求菱形ABEF的面积．
【答案】（1）见解析；（2）8
【解析】
（1）先利用角平分线的性质和平行线的性质得出四边形ABEF是平行四边形，再利用两邻边相等即可证明四边形ABEF是菱形；
（2）连结BF，交AE于G,先利用菱形的性质和特殊角的三角函数值求出BF的长度，然后利用菱形的面积公式
即可求解．
解：（1）∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠EAF＝∠AEB，
∵∠EAB＝∠EAF，
∴∠EAB＝∠AEB．
∴BE＝AB＝AF．
∵AF∥BE，
∴四边形ABEF是平行四边形，
∵AB＝BE，
∴四边形ABEF是菱形；
（2）如图，连结BF，交AE于G．
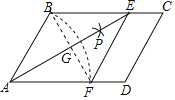
∵四边形ABCD是平行四边形，
∴∠BAD＝∠C＝60°，
∵四边形ABEF 菱形，
∴BF⊥AE，AG＝EG＝
2，∠BAG＝∠FAG＝
30°，
∴BG＝FG＝AGtan30°＝2，
∴BF＝4，
∴菱形ABEF的面积＝
．
练习册系列答案
特高级教师点拨系列答案
相关题目
