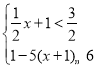题目内容
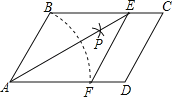
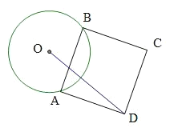
【题目】如图,⊙O 的半径为 3,AB 为圆上一动弦,以 AB 为边作正方形 ABCD,求 OD 的最大值__.
【答案】3![]() +3
+3
【解析】
把AO绕点A顺时针旋转90![]() 得到AO′,得到△AOO′是等腰直角三角形,根据等腰直角三角形的性质求出OO′,再根据正方形的性质可得AB=AD,再求出∠BAO=∠DAO′,然后利用“边角边”证明△ABO和△ADO′全等,根据全等三角形对应边相等可得DO′=BO,再根据三角形的任意两边之和大于第三边求解即可.
得到AO′,得到△AOO′是等腰直角三角形,根据等腰直角三角形的性质求出OO′,再根据正方形的性质可得AB=AD,再求出∠BAO=∠DAO′,然后利用“边角边”证明△ABO和△ADO′全等,根据全等三角形对应边相等可得DO′=BO,再根据三角形的任意两边之和大于第三边求解即可.
如图,连接AO、BO、把AO绕点A顺时针旋转90![]() 得到AO′,连接DO’
得到AO′,连接DO’
∴△AOO′是等腰直角三角形,
∵AO=3,
∴OO′=![]() =3
=3![]() ,
,
在正方形ABCD中,AB=AD,∠BAD=90![]() ,
,
∵∠BAO+∠BAO′=∠DAO′+∠BAO′=90![]() ,
,
∴∠BAO=∠DAO′,
在△ABO和△ADO′,
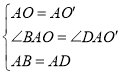 ,
,
∴△ABO≌△ADO′(SAS),
∴DO′=BO=3,
∴OO′+O′D≥OD,
当O、O′、D三点共线时,取“=”,
此时,OD的最大值为3![]() +3.
+3.
故答案为:3![]() +3.
+3.

练习册系列答案
相关题目
【题目】小明经过市场调查,整理出他妈妈商店里一种商品在第![]() 天的销售量的相关信息如下表:
天的销售量的相关信息如下表:
时间第 |
|
|
售价(元/件) |
| 50 |
每天销量(件) |
| |
已知该商品的进价为每件20元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.