题目内容
【题目】如图,正方形纸片ABCD沿直线BE折叠,点C恰好落在点G处,连接BG并延长,交CD于点H,延长EG交AD于点F,连接FH.若AF=FD=6cm,则FH的长为_____cm.
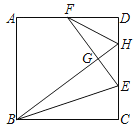
【答案】3![]()
【解析】
连接BF,先证明Rt△ABF≌Rt△GBF,得到∠AFB=∠GFB,FA=FG,再证明Rt△FGH≌Rt△FDH,得到∠GFH=∠DFH,于是∠BFH=∠BFG+∠GFH=![]() ×180°=90°,根据△ABF∽△DFH,得
×180°=90°,根据△ABF∽△DFH,得![]() ,从而可求出FH.
,从而可求出FH.
解:如图,连接BF.
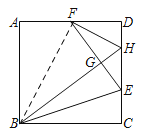
∵四边形ABCD是正方形,
∴∠A=∠C=90°,AB=BC=AF+FD=12cm.
由折叠可知,BG=BC=12cm,∠BGE=∠BCE=90°.
∴AB=GB.
在Rt△ABF和Rt△GBF中,
![]() ,
,
∴Rt△ABF≌Rt△GBF(HL).
∴∠AFB=∠GFB,FA=FG,
又∵AF=FD,
∴FG=FD.
同理可证Rt△FGH≌Rt△FDH,
∴∠GFH=∠DFH,
∴∠BFH=∠BFG+∠GFH=![]() 180°=90°,
180°=90°,
∴∠AFB+∠DFH=90°.
又∵∠AFB+∠ABF=90°,
∴∠ABF=∠DFH.
又∵∠A=∠D=90°,
∴△ABF∽△DFH,
∴![]() ,
,
在Rt△ABF中,由勾股定理,得BF=![]()
![]() ,
,
∴![]() ,
,
∴FH=![]() .
.
故答案为:3![]() .
.

 阅读快车系列答案
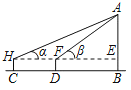
阅读快车系列答案【题目】舍利生生塔位于晋祠南瑞,建于隋开皇年间,宋代重修,清乾隆十六年(1751年)重建.七屋八角,琉璃瓦顶,远远望去,高耸的古塔,映衬着蓝天白云,甚是壮观.原塔内每层均有佛像,开4门8窗,凭窗远眺,晋祠内外美景可一览无余.如果在夕阳西下时欣赏宝塔,还会出现——天云锦、满塔光辉的壮丽景观,被誉为“宝塔披霞”.某数学“综合与实践”小组的同学把“测量舍利生生塔高”作为一项课题活动,他们制定了测量方案,并利用课余时间完成了实地测量,测量结果如表:
课题 | 测量舍利生生塔高 | |||
测量示意图 |
| 说明:某同学在地面上选择点C,使用手持测角仪,测得此时楼顶A的仰角∠AHE=α,沿CB方向前进到点D,测量出C,D之间的距离CD=xm,在点D使用手持测角仪,测得此时楼顶A的仰角∠AFE=β | ||
测量数据 | α的度数 | β的度数 | CD的长度 | 该同学眼睛离地面的距离HC |
24° | 37° | 32m | 1.76m | |
… | … | |||
(1)请帮助该小组的同学根据上表中的测量数据,求塔高AB.(结果精确到1m;参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(2)该小组要写出一份完整的课题活动报告,除上表中的项目外,你认为还需要补充哪些项目?(写出一个即可)

【题目】小明经过市场调查,整理出他妈妈商店里一种商品在第![]() 天的销售量的相关信息如下表:
天的销售量的相关信息如下表:
时间第 |
|
|
售价(元/件) |
| 50 |
每天销量(件) |
| |
已知该商品的进价为每件20元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.